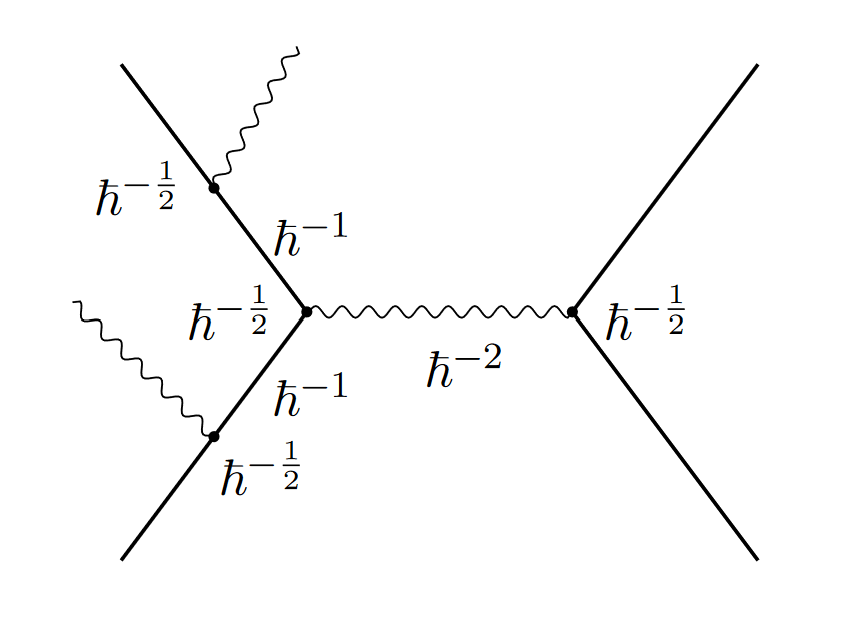Tag Archives: amplitudes

Cabinet of Curiosities: The Cubic

Before I launch into the post: I got interviewed on Theoretically Podcasting, a new YouTube channel focused on beginning grad student-level explanations of topics in theoretical physics. If that sounds interesting to you, check it out!

This Fall is paper season for me. I’m finishing up a number of different projects, on a number of different things. Each one was its own puzzle: a curious object found, polished, and sent off into the world.

Monday I published the first of these curiosities, along with Jake Bourjaily and Cristian Vergu.

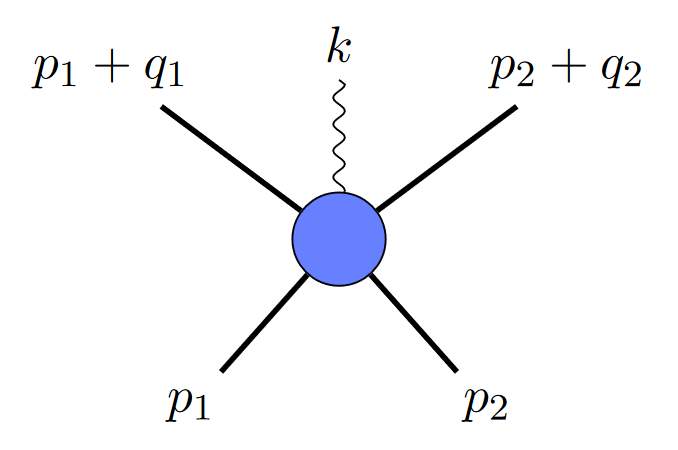
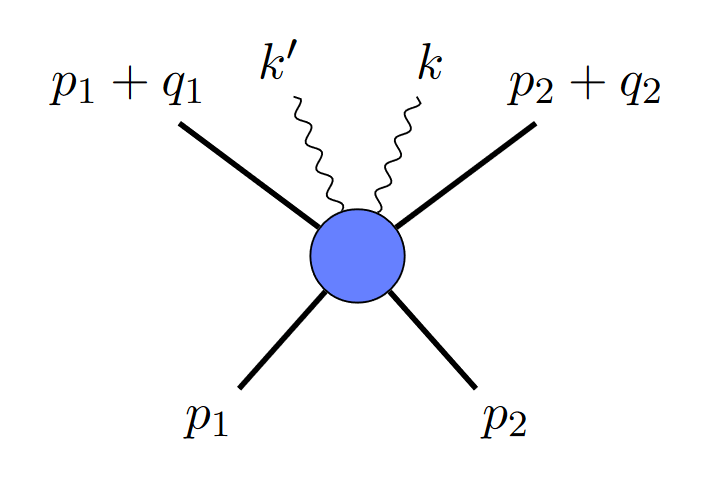
I’ve mentioned before that the calculations I do involve a kind of “alphabet“. Break down a formula for the probability that two particles collide, and you find pieces that occur again and again. In the nicest cases, those pieces are rational functions, but they can easily get more complicated. I’ve talked before about a case where square roots enter the game, for example. But if square roots appear, what about something even more complicated? What about cubic roots?

Occasionally, my co-authors and I would say something like that at the end of a talk and an older professor would scoff: “Cube roots? Impossible!”

You might imagine these professors were just being unreasonable skeptics, the elderly-but-distinguished scientists from that Arthur C. Clarke quote. But while they turned out to be wrong, they weren’t being unreasonable. They were thinking back to theorems from the 60’s, theorems which seemed to argue that these particle physics calculations could only have a few specific kinds of behavior: they could behave like rational functions, like logarithms, or like square roots. Theorems which, as they understood them, would have made our claims impossible.

Eventually, we decided to figure out what the heck was going on here. We grabbed the simplest example we could find (a cube root involving three loops and eleven gluons in N=4 super Yang-Mills…yeah) and buckled down to do the calculation.

When we want to calculate something specific to our field, we can reference textbooks and papers, and draw on our own experience. Much of the calculation was like that. A crucial piece, though, involved something quite a bit less specific: calculating a cubic root. And for things like that, you can tell your teachers we use only the very best: Wikipedia.

Check out the Wikipedia entry for the cubic formula. It’s complicated, in ways the quadratic formula isn’t. It involves complex numbers, for one. But it’s not that crazy.

What those theorems from the 60’s said (and what they actually said, not what people misremembered them as saying), was that you can’t take a single limit of a particle physics calculation, and have it behave like a cubic root. You need to take more limits, not just one, to see it.

It turns out, you can even see this just from the Wikipedia entry. There’s a big cube root sign in the middle there, equal to some variable “C”. Look at what’s inside that cube root. You want that part inside to vanish. That means two things need to cancel: Wikipedia labels them $\Delta_1$ , and $\sqrt{\Delta_1^2-4\Delta_0^3}$ . Do some algebra, and you’ll see that for those to cancel, you need $\Delta_0=0$ .

So you look at the limit, $\Delta_0\rightarrow 0$ . This time you need not just some algebra, but some calculus. I’ll let the students in the audience work it out, but at the end of the day, you should notice how C behaves when $\Delta_0$ is small. It isn’t like $\sqrt[3]{\Delta_0}$ . It’s like just plain $\Delta_0$ . The cube root goes away.

It can come back, but only if you take another limit: not just $\Delta_0\rightarrow 0$ , but $\Delta_1\rightarrow 0$ as well. And that’s just fine according to those theorems from the 60’s. So our cubic curiosity isn’t impossible after all.

Our calculation wasn’t quite this simple, of course. We had to close a few loopholes, checking our example in detail using more than just Wikipedia-based methods. We found what we thought was a toy example, that turned out to be even more complicated, involving roots of a degree-six polynomial (one that has no “formula”!).

And in the end, polished and in their display case, we’ve put our examples up for the world to see. Let’s see what people think of them!

Why the Antipode Was Supposed to Be Useless

13 Replies

A few weeks back, Quanta Magazine had an article about a new discovery in my field, called antipodal duality.

Some background: I’m a theoretical physicist, and I work on finding better ways to make predictions in particle physics. Folks in my field make these predictions with formulas called “scattering amplitudes” that encode the probability that particles bounce, or scatter, in particular ways. One trick we’ve found is that these formulas can often be written as “words” in a kind of “alphabet”. If we know the alphabet, we can make our formulas much simpler, or even guess formulas we could never have calculated any other way.

Quanta’s article describes how a few friends of mine (Lance Dixon, Ömer Gürdoğan, Andrew McLeod, and Matthias Wilhelm) noticed a weird pattern in two of these formulas, from two different calculations. If you flip the “words” around, back to front (an operation called the antipode), you go from a formula describing one collision of particles to a formula for totally different particles. Somehow, the two calculations are “dual”: two different-seeming descriptions that secretly mean the same thing.

Quanta quoted me for their article, and I was (pleasantly) baffled. See, the antipode was supposed to be useless. The mathematicians told us it was something the math allows us to do, like you’re allowed to order pineapple on pizza. But just like pineapple on pizza, we couldn’t imagine a situation where we actually wanted to do it.

What Quanta didn’t say was why we thought the antipode was useless. That’s a hard story to tell, one that wouldn’t fit in a piece like that.

It fits here, though. So in the rest of this post, I’d like to explain why flipping around words is such a strange, seemingly useless thing to do. It’s strange because it swaps two things that in physics we thought should be independent: branch cuts and derivatives, or particles and symmetries.

Let’s start with the first things in each pair: branch cuts, and particles.

The first few letters of our “word” tell us something mathematical, and they tell us something physical. Mathematically, they tell us ways that our formula can change suddenly, and discontinuously.

Take a logarithm, the inverse of $e^x$ . You’re probably used to plugging in positive numbers, and getting out something reasonable, that changes in a smooth and regular way: after all, $e^x$ is always positive, right? But in mathematics, you don’t have to just use positive numbers. You can use negative numbers. Even more interestingly, you can use complex numbers. And if you take the logarithm of a complex number, and look at the imaginary part, it looks like this:

Mostly, this complex logarithm still seems to be doing what it’s supposed to, changing in a nice slow way. But there is a weird “cut” in the graph for negative numbers: a sudden jump, from $\pi$ to $-\pi$ . That jump is called a “branch cut”.

As physicists, we usually don’t like our formulas to make sudden changes. A change like this is an infinitely fast jump, and we don’t like infinities much either. But we do have one good use for a formula like this, because sometimes our formulas do change suddenly: when we have enough energy to make a new particle.

Imagine colliding two protons together, like at the LHC. Colliding particles doesn’t just break the protons into pieces: due to Einstein’s famous $E=mc^2$ , it can create new particles as well. But to create a new particle, you need enough energy: $mc^2$ worth of energy. So as you dial up the energy of your protons, you’ll notice a sudden change: you couldn’t create, say, a Higgs boson, and now you can. Our formulas represent some of those kinds of sudden changes with branch cuts.

So the beginning of our “words” represent branch cuts, and particles. The end represents derivatives and symmetries.

Derivatives come from the land of calculus, a place spooky to those with traumatic math class memories. Derivatives shouldn’t be so spooky though. They’re just ways we measure change. If we have a formula that is smoothly changing as we change some input, we can describe that change with a derivative.

The ending of our “words” tell us what happens when we take a derivative. They tell us which ways our formulas can smoothly change, and what happens when they do.

In doing so, they tell us about something some physicists make sound spooky, called symmetries. Symmetries are changes we can make that don’t really change what’s important. For example, you could imagine lifting up the entire Large Hadron Collider and (carefully!) carrying it across the ocean, from France to the US. We’d expect that, once all the scared scientists return and turn it back on, it would start getting exactly the same results. Physics has “translation symmetry”: you can move, or “translate” an experiment, and the important stuff stays the same.

These symmetries are closely connected to derivatives. If changing something doesn’t change anything important, that should be reflected in our formulas: they shouldn’t change either, so their derivatives should be zero. If instead the symmetry isn’t quite true, if it’s what we call “broken”, then by knowing how it was “broken” we know what the derivative should be.

So branch cuts tell us about particles, derivatives tell us about symmetries. The weird thing about the antipode, the un-physical bizarre thing, is that it swaps them. It makes the particles of one calculation determine the symmetries of another.

(And lest you’ve heard about particles with symmetries, like gluons and SU(3)…this is a different kind of thing. I don’t have enough room to explain why here, but it’s completely unrelated.)

Why the heck does this duality exist?

A commenter on the last post asked me to speculate. I said there that I have no clue, and that’s most of the answer.

If I had to speculate, though, my answer might be disappointing.

Most of the things in physics we call “dualities” have fairly deep physical meanings, linked to twisting spacetime in complicated ways. AdS/CFT isn’t fully explained, but it seems to be related to something called the holographic principle, the idea that gravity ties together the inside of space with the boundary around it. T duality, an older concept in string theory, is explained: a consequence of how strings “see” the world in terms of things to wrap around and things to spin around. In my field, one of our favorite dualities links back to this as well, amplitude-Wilson loop duality linked to fermionic T-duality.

The antipode doesn’t twist spacetime, it twists the mathematics. And it may be it matters only because the mathematics is so constrained that it’s forced to happen.

The trick that Lance Dixon and co. used to discover antipodal duality is the same trick I used with Lance to calculate complicated scattering amplitudes. It relies on taking a general guess of words in the right “alphabet”, and constraining it: using mathematical and physical principles it must obey and throwing out every illegal answer until there’s only one answer left.

Currently, there are some hints that the principles used for the different calculations linked by antipodal duality are “antipodal mirrors” of each other: that different principles have the same implication when the duality “flips” them around. If so, then it could be this duality is in some sense just a coincidence: not a coincidence limited to a few calculations, but a coincidence limited to a few principles. Thought of in this way, it might not tell us a lot about other situations, it might not really be “deep”.

Of course, I could be wrong about this. It could be much more general, could mean much more. But in that context, I really have no clue what to speculate. The antipode is weird: it links things that really should not be physically linked. We’ll have to see what that actually means.

Amplitudes 2022 Retrospective

3 Replies

I’m back from Amplitudes 2022 with more time to write, and (besides the several papers I’m working on) that means writing about the conference! Casual readers be warned, there’s no way around this being a technical post, I don’t have the space to explain everything!

I mostly said all I wanted about the way the conference was set up in last week’s post, but one thing I didn’t say much about was the conference dinner. Most conference dinners are the same aside from the occasional cool location or haggis speech. This one did have a cool location, and a cool performance by a blind pianist, but the thing I really wanted to comment on was the setup. Typically, the conference dinner at Amplitudes is a sit-down affair: people sit at tables in one big room, maybe getting up occasionally to pick up food, and eventually someone gives an after-dinner speech. This time the tables were standing tables, spread across several rooms. This was a bit tiring on a hot day, but it did have the advantage that it naturally mixed people around. Rather than mostly talking to “your table”, you’d wander, ending up at a new table every time you picked up new food or drinks. It was a good way to meet new people, a surprising number of which in my case apparently read this blog. It did make it harder to do an after-dinner speech, so instead Lance gave an after-conference speech, complete with the now-well-established running joke where Greta Thunberg tries to get us to fly less.

(In another semi-running joke, the organizers tried to figure out who had attended the most of the yearly Amplitudes conferences over the years. Weirdly, no-one has attended all twelve.)

In terms of the content, and things that stood out:

Nima is getting close to publishing his newest ‘hedron, the surfacehedron, and correspondingly was able to give a lot more technical detail about it. (For his first and most famous amplituhedron, see here.) He still didn’t have enough time to explain why he has to use category theory to do it, but at least he was concrete enough that it was reasonably clear where the category theory was showing up. (I wasn’t there for his eight-hour lecture at the school the week before, maybe the students who stuck around until 2am learned some category theory there.) Just from listening in on side discussions, I got the impression that some of the ideas here actually may have near-term applications to computing Feynman diagrams: this hasn’t been a feature of previous ‘hedra and it’s an encouraging development.

Alex Edison talked about progress towards this blog’s namesake problem, the question of whether N=8 supergravity diverges at seven loops. Currently they’re working at six loops on the N=4 super Yang-Mills side, not yet in a form it can be “double-copied” to supergravity. The tools they’re using are increasingly sophisticated, including various slick tricks from algebraic geometry. They are looking to the future: if they’re hoping their methods will reach seven loops, the same methods have to make six loops a breeze.

Xi Yin approached a puzzle with methods from String Field Theory, prompting the heretical-for-us title “on-shell bad, off-shell good”. A colleague reminded me of a local tradition for dealing with heretics.

While Nima was talking about a new ‘hedron, other talks focused on the original amplituhedron. Paul Heslop found that the amplituhedron is not literally a positive geometry, despite slogans to the contrary, but what it is is nonetheless an interesting generalization of the concept. Livia Ferro has made more progress on her group’s momentum amplituhedron: previously only valid at tree level, they now have a picture that can accomodate loops. I wasn’t sure this would be possible, there are a lot of things that work at tree level and not for loops, so I’m quite encouraged that this one made the leap successfully.

Sebastian Mizera, Andrew McLeod, and Hofie Hannesdottir all had talks that could be roughly summarized as “deep principles made surprisingly useful”. Each took topics that were explored in the 60’s and translated them into concrete techniques that could be applied to modern problems. There were surprisingly few talks on the completely concrete end, on direct applications to collider physics. I think Simone Zoia’s was the only one to actually feature collider data with error bars, which might explain why I singled him out to ask about those error bars later.

Likewise, Matthias Wilhelm’s talk was the only one on functions beyond polylogarithms, the elliptic functions I’ve also worked on recently. I wonder if the under-representation of some of these topics is due to the existence of independent conferences: in a year when in-person conferences are packed in after being postponed across the pandemic, when there are already dedicated conferences for elliptics and practical collider calculations, maybe people are just a bit too tired to go to Amplitudes as well.

Talks on gravitational waves seem to have stabilized at roughly a day’s worth, which seems reasonable. While the subfield’s capabilities continue to be impressive, it’s also interesting how often new conceptual challenges appear. It seems like every time a challenge to their results or methods is resolved, a new one shows up. I don’t know whether the field will ever get to a stage of “business as usual”, or whether it will be novel qualitative questions “all the way up”.

I haven’t said much about the variety of talks bounding EFTs and investigating their structure, though this continues to be an important topic. And I haven’t mentioned Lance Dixon’s talk on antipodal duality, largely because I’m planning a post on it later: Quanta Magazine had a good article on it, but there are some aspects even Quanta struggled to cover, and I think I might have a good way to do it.

At Amplitudes 2022 in Prague

The Conference Dilemma: Freshness vs. Breadth

Carving Out the Possible

8 Replies

If you imagine a particle physicist, you probably picture someone spending their whole day dreaming up new particles. They figure out how to test those particles in some big particle collider, and for a lucky few their particle gets discovered and they get a Nobel prize.

Occasionally, a wiseguy asks if we can’t just cut out the middleman. Instead of dreaming up particles to test, why don’t we just write down every possible particle and test for all of them? It would save the Nobel committee a lot of money at least!

It turns out, you can sort of do this, through something called Effective Field Theory. An Effective Field Theory is a type of particle physics theory that isn’t quite true: instead, it’s “effectively” true, meaning true as long as you don’t push it too far. If you test it at low energies and don’t “zoom in” too much then it’s fine. Crank up your collider energy high enough, though, and you expect the theory to “break down”, revealing new particles. An Effective Field Theory lets you “hide” unknown particles inside new interactions between the particles we already know.

To help you picture how this works, imagine that the pink and blue lines here represent familiar particles like electrons and quarks, while the dotted line is a new particle somebody dreamed up. (The picture is called a Feynman diagram, if you don’t know what that is check out this post.)

In an Effective Field Theory, we “zoom out”, until the diagram looks like this:

Now we’ve “hidden” the new particle. Instead, we have a new type of interaction between the particles we already know.

So instead of writing down every possible new particle we can imagine, we only have to write down every possible interaction between the particles we already know.

That’s not as hard as it sounds. In part, that’s because not every interaction actually makes sense. Some of the things you could write down break some important rules. They might screw up cause and effect, letting something happen before its cause instead of after. They might screw up probability, giving you a formula for the chance something happens that gives a number greater than 100%.

Using these rules you can play a kind of game. You start out with a space representing all of the interactions you can imagine. You begin chipping at it, carving away parts that don’t obey the rules, and you see what shape is left over. You end up with plots that look a bit like carving a ham.

People in my subfield are getting good at this kind of game. It isn’t quite our standard fare: usually, we come up with tricks to make calculations with specific theories easier. Instead, many groups are starting to look at these general, effective theories. We’ve made friends with groups in related fields, building new collaborations. There still isn’t one clear best way to do this carving, so each group manages to find a way to chip a little farther. Out of the block of every theory we could imagine, we’re carving out a space of theories that make sense, theories that could conceivably be right. Theories that are worth testing.

Of Snowmass and SAGEX

2 Replies

arXiv-watchers might have noticed an avalanche of papers with the word Snowmass in the title. (I contributed to one of them.)

Snowmass is a place, an area in Colorado known for its skiing. It’s also an event in that place, the Snowmass Community Planning Exercise for the American Physical Society’s Division of Particles and Fields. In plain terms, it’s what happens when particle physicists from across the US get together in a ski resort to plan their future.

Usually someone like me wouldn’t be involved in that. (And not because it’s a ski resort.) In the past, these meetings focused on plans for new colliders and detectors. They got contributions from experimentalists, and a few theorists heavily focused on their work, but not the more “formal” theorists beyond.

This Snowmass is different. It’s different because of Corona, which changed it from a big meeting in a resort to a spread-out series of meetings and online activities. It’s also different because they invited theorists to contribute, and not just those interested in particle colliders. The theorists involved study everything from black holes and quantum gravity to supersymmetry and the mathematics of quantum field theory. Groups focused on each topic submit “white papers” summarizing the state of their area. These white papers in turn get organized and summarized into a few subfields, which in turn contribute to the planning exercise. No-one I’ve talked to is entirely clear on how this works, how much the white papers will actually be taken into account or by whom. But it seems like a good chance to influence US funding agencies, like the Department of Energy, and see if we can get them to prioritize our type of research.

Europe has something similar to Snowmass, called the European Strategy for Particle Physics. It also has smaller-scale groups, with their own purposes, goals, and funding sources. One such group is called SAGEX: Scattering Amplitudes: from Geometry to EXperiment. SAGEX is an Innovative Training Network, an organization funded by the EU to train young researchers, in this case in scattering amplitudes. Its fifteen students are finishing their PhDs and ready to take the field by storm. Along the way, they spent a little time in industry internships (mostly at Maple and Mathematica), and quite a bit of time working on outreach.

They have now summed up that outreach work in an online exhibition. I’ve had fun exploring it over the last couple days. They’ve got a lot of good content there, from basic explanations of relativity and quantum mechanics, to detailed games involving Feynman diagrams and associahedra, to a section that uses solitons as a gentle introduction to integrability. If you’re in the target audience, you should check it out!

Geometry and Geometry

Classicality Has Consequences

16 Replies

Last week, I mentioned some interesting new results in my corner of physics. I’ve now finally read the two papers and watched the recorded talk, so I can satisfy my frustrated commenters.

Quantum mechanics is a very cool topic and I am much less qualified than you would expect to talk about it. I use quantum field theory, which is based on quantum mechanics, so in some sense I use quantum mechanics every day. However, most of the “cool” implications of quantum mechanics don’t come up in my work. All the debates about whether measurement “collapses the wavefunction” are irrelevant when the particles you measure get absorbed in a particle detector, never to be seen again. And while there are deep questions about how a classical world emerges from quantum probabilities, they don’t matter so much when all you do is calculate those probabilities.

They’ve started to matter, though. That’s because quantum field theorists like me have recently started working on a very different kind of problem: trying to predict the output of gravitational wave telescopes like LIGO. It turns out you can do almost the same kind of calculation we’re used to: pretend two black holes or neutron stars are sub-atomic particles, and see what happens when they collide. This trick has grown into a sub-field in its own right, one I’ve dabbled in a bit myself. And it’s gotten my kind of physicists to pay more attention to the boundary between classical and quantum physics.

The thing is, the waves that LIGO sees really are classical. Any quantum gravity effects there are tiny, undetectably tiny. And while this doesn’t have the implications an expert might expect (we still need loop diagrams), it does mean that we need to take our calculations to a classical limit.

Figuring out how to do this has been surprisingly delicate, and full of unexpected insight. A recent example involves two papers, one by Andrea Cristofoli, Riccardo Gonzo, Nathan Moynihan, Donal O’Connell, Alasdair Ross, Matteo Sergola, and Chris White, and one by Ruth Britto, Riccardo Gonzo, and Guy Jehu. At first I thought these were two groups happening on the same idea, but then I noticed Riccardo Gonzo on both lists, and realized the papers were covering different aspects of a shared story. There is another group who happened upon the same story: Paolo Di Vecchia, Carlo Heissenberg, Rodolfo Russo and Gabriele Veneziano. They haven’t published yet, so I’m basing this on the Gonzo et al papers.

The key question each group asked was, what does it take for gravitational waves to be classical? One way to ask the question is to pick something you can observe, like the strength of the field, and calculate its uncertainty. Classical physics is deterministic: if you know the initial conditions exactly, you know the final conditions exactly. Quantum physics is not. What should happen is that if you calculate a quantum uncertainty and then take the classical limit, that uncertainty should vanish: the observation should become certain.

Another way to ask is to think about the wave as made up of gravitons, particles of gravity. Then you can ask how many gravitons are in the wave, and how they are distributed. It turns out that you expect them to be in a coherent state, like a laser, one with a very specific distribution called a Poisson distribution: a distribution in some sense right at the border between classical and quantum physics.

The results of both types of questions were as expected: the gravitational waves are indeed classical. To make this work, though, the quantum field theory calculation needs to have some surprising properties.

If two black holes collide and emit a gravitational wave, you could depict it like this:

where the straight lines are black holes, and the squiggly line is a graviton. But since gravitational waves are made up of multiple gravitons, you might ask, why not depict it with two gravitons, like this?

It turns out that diagrams like that are a problem: they mean your two gravitons are correlated, which is not allowed in a Poisson distribution. In the uncertainty picture, they also would give you non-zero uncertainty. Somehow, in the classical limit, diagrams like that need to go away.

And at first, it didn’t look like they do. You can try to count how many powers of Planck’s constant show up in each diagram. The authors do that, and it certainly doesn’t look like it goes away:

An example from the paper with Planck’s constants sprinkled around

Luckily, these quantum field theory calculations have a knack for surprising us. Calculate each individual diagram, and things look hopeless. But add them all together, and they miraculously cancel. In the classical limit, everything combines to give a classical result.

You can do this same trick for diagrams with more graviton particles, as many as you like, and each time it ought to keep working. You get an infinite set of relationships between different diagrams, relationships that have to hold to get sensible classical physics. From thinking about how the quantum and classical are related, you’ve learned something about calculations in quantum field theory.

That’s why these papers caught my eye. A chunk of my sub-field is needing to learn more and more about the relationship between quantum and classical physics, and it may have implications for the rest of us too. In the future, I might get a bit more qualified to talk about some of the very cool implications of quantum mechanics.

Science, Gifts Enough for Lifetimes

7 Replies

Merry Newtonmas, Everyone!

In past years, I’ve compared science to a gift: the ideal gift for the puzzle-fan, one that keeps giving new puzzles. I think people might not appreciate the scale of that gift, though.

Bigger than all the creative commons Wikipedia images

Maybe you’ve heard the old joke that studying for a PhD means learning more and more about less and less until you know absolutely everything about nothing at all. This joke is overstating things: even when you’ve specialized down to nothing at all, you still won’t know everything.

If you read the history of science, it might feel like there are only a few important things going on at a time. You notice the simultaneous discoveries, like calculus from Newton and Liebniz and natural selection from Darwin and Wallace. You can get the impression that everyone was working on a few things, the things that would make it into the textbooks. In fact, though, there was always a lot to research, always many interesting things going on at once. As a scientist, you can’t escape this. Even if you focus on your own little area, on a few topics you care about, even in a small field, there will always be more going on than you can keep up with.

This is especially clear around the holiday season. As everyone tries to get results out before leaving on vacation, there is a tidal wave of new content. I have five papers open on my laptop right now (after closing four or so), and some recorded talks I keep meaning to watch. Two of the papers are the kind of simultaneous discovery I mentioned: two different groups noticing that what might seem like an obvious fact – that in classical physics, unlike in quantum, one can have zero uncertainty – has unexpected implications for our kind of calculations. (A third group got there too, but hasn’t published yet.) It’s a link I would never have expected, and with three groups coming at it independently you’d think it would be the only thing to pay attention to: but even in the same sub-sub-sub-field, there are other things going on that are just as cool! It’s wild, and it’s not some special quirk of my area: that’s science, for all us scientists. No matter how much you expect it to give you, you’ll get more, lifetimes and lifetimes worth. That’s a Newtonmas gift to satisfy anyone.

4 gravitons

Stories about physics from someone who's been there