Tag Archives: DoingScience

Cabinet of Curiosities: The Deluxe Train Set

Leave a reply

I’ve got a new paper out this week with Andrew McLeod. I’m thinking of it as another entry in this year’s “cabinet of curiosities”, interesting Feynman diagrams with unusual properties. Although this one might be hard to fit into a cabinet.

Over the past few years, I’ve been finding Feynman diagrams with interesting connections to Calabi-Yau manifolds, the spaces originally studied by string theorists to roll up their extra dimensions. With Andrew and other collaborators, I found an interesting family of these diagrams called traintracks, which involve higher-and-higher dimensional manifolds as they get longer and longer.

This time, we started hooking up our traintracks together.

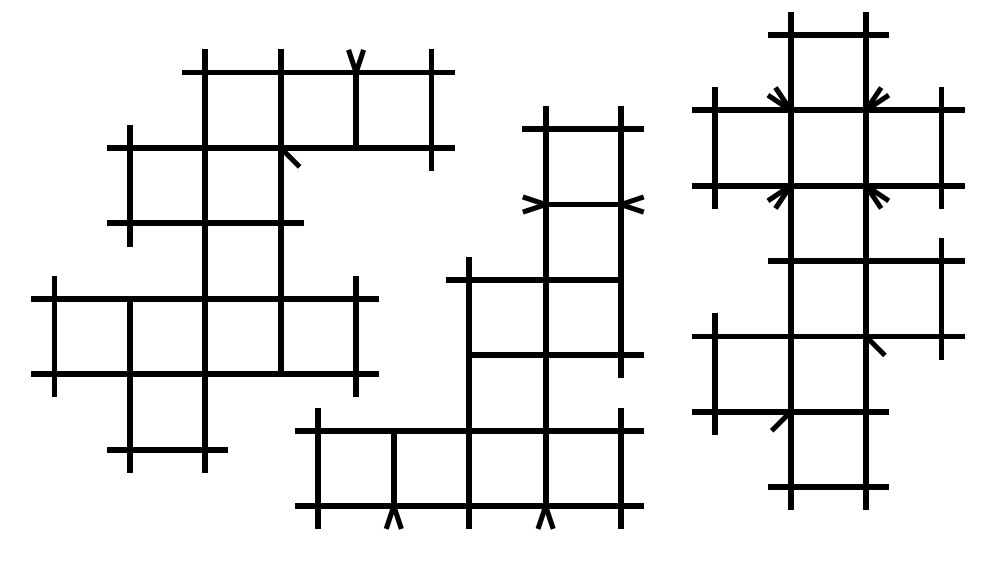
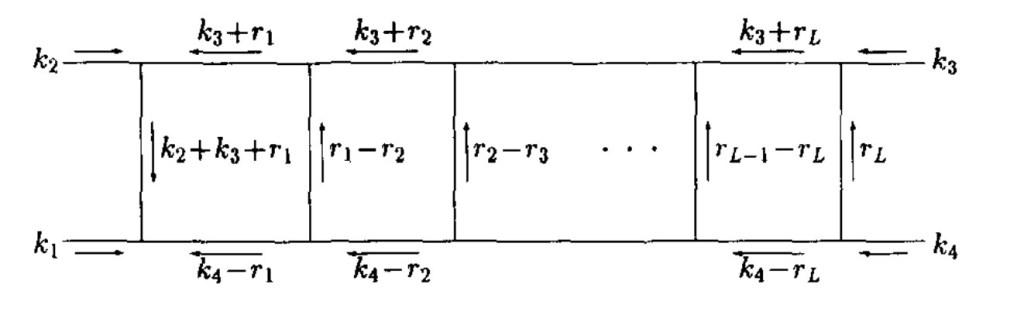
We call diagrams like these traintrack network diagrams, or traintrack networks for short. The original traintracks just went “one way”: one family, going higher in Calabi-Yau dimension the longer they got. These networks branch out, one traintrack leading to another and another.

In principle, these are much more complicated diagrams. But we find we can work with them in almost the same way. We can find the same “starting point” we had for the original traintracks, the set of integrals used to find the Calabi-Yau manifold. We’ve even got more reliable tricks, a method recently honed by some friends of ours that consistently find a Calabi-Yau manifold inside the original traintracks.

Surprisingly, though, this isn’t enough.

It works for one type of traintrack network, a so-called “cross diagram” like this:

But for other diagrams, if the network branches any more, the trick stops working. We still get an answer, but that answer is some more general space, not just a Calabi-Yau manifold.

That doesn’t mean that these general traintrack networks don’t involve Calabi-Yaus at all, mind you: it just means this method doesn’t tell us one way or the other. It’s also possible that simpler versions of these diagrams, involving fewer particles, will once again involve Calabi-Yaus. This is the case for some similar diagrams in two dimensions. But it’s starting to raise a question: how special are the Calabi-Yau related diagrams? How general do we expect them to be?

Another fun thing we noticed has to do with differential equations. There are equations that relate one diagram to another simpler one. We’ve used them in the past to build up “ladders” of diagrams, relating each picture to one with one of its boxes “deleted”. We noticed, playing with these traintrack networks, that these equations do a bit more than we thought. “Deleting” a box can make a traintrack short, but it can also chop a traintrack in half, leaving two “dangling” pieces, one on either side.

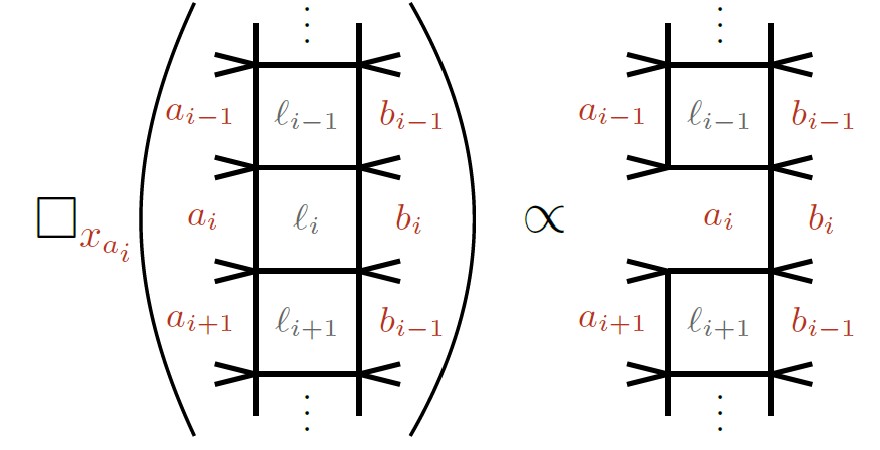
This reminded me of an important point, one we occasionally lose track of. The best-studied diagrams related to Calabi-Yaus are called “sunrise” diagrams. If you squish together a loop in one of those diagrams, the whole diagram squishes together, becoming much simpler. Because of that, we’re used to thinking of these as diagrams with a single “geometry”, one that shows up when you don’t “squish” anything.

Traintracks, and traintrack networks, are different. “Squishing” the diagram, or “deleting” a box, gives you a simpler diagram, but not much simpler. In particular, the new diagram will still contain traintracks, and traintrack networks. That means that we really should think of each traintrack network not just as one “top geometry”, but of a collection of geometries, different Calabi-Yaus that break into different combinations of Calabi-Yaus in different ways. It’s something we probably should have anticipated, but the form these networks take is a good reminder, one that points out that we still have a lot to do if we want to understand these diagrams.

Learning for a Living

Leave a reply

It’s a question I’ve now heard several times, in different forms. People hear that I’ll be hired as a researcher at an institute of theoretical physics, and they ask, “what, exactly, are they paying you to research?”

The answer, with some caveats: “Whatever I want.”

When a company hires a researcher, they want to accomplish specific things: to improve their products, to make new ones, to cut down on fraud or out-think the competition. Some government labs are the same: if you work for NIST, for example, your work should contribute in some way to achieving more precise measurements and better standards for technology.

Other government labs, and universities, are different. They pursue basic research, research not on any specific application but on the general principles that govern the world. Researchers doing basic research are given a lot of freedom, and that freedom increases as their careers go on.

As a PhD student, a researcher is a kind of apprentice, working for their advisor. Even then, they have some independence: an advisor may suggest projects, but PhD students usually need to decide how to execute them on their own. In some fields, there can be even more freedom: in theoretical physics, it’s not unusual for the more independent students to collaborate with other people than just their advisor.

Postdocs, in turn, have even more freedom. In some fields they get hired to work on a specific project, but they tend to have more freedom as to how to execute it than a PhD student would. Other fields give them more or less free rein: in theoretical physics, a postdoc will have some guidance, but often will be free to work on whatever they find interesting.

Professors, and other long-term researchers, have the most freedom of all. Over the climb from PhD to postdoc to professor, researchers build judgement, demonstrating a track record for tackling worthwhile scientific problems. Universities, and institutes of basic research, trust that judgement. They hire for that judgement. They give their long-term researchers free reign to investigate whatever questions they think are valuable.

In practice, there are some restrictions. Usually, you’re supposed to research in a particular field: at an institute for theoretical physics, I should probably research theoretical physics. (But that can mean many things: one of my future colleagues studies the science of cities.) Further pressure comes from grant funding, money you need to hire other researchers or buy equipment that can come with restrictions attached. When you apply for a grant, you have to describe what you plan to do. (In practice, grant agencies are more flexible about this than you might expect, allowing all sorts of changes if you have a good reason…but you still can’t completely reinvent yourself.) Your colleagues themselves also have an impact: it’s much easier to work on something when you can walk down the hall and ask an expert when you get stuck. It’s why we seek out colleagues who care about the same big questions as we do.

Overall, though, research is one of the free-est professions there is. If you can get a job learning for a living, and do it well enough, then people will trust your judgement. They’ll set you free to ask your own questions, and seek your own answers.

Enfin, Permanent

10 Replies

My blog began, almost eleven years ago, with the title “Four Gravitons and a Grad Student”. Since then, I finished my PhD. The “Grad Student” dropped from the title, and the mysterious word “postdoc” showed up on a few pages. For three years I worked as a postdoc at the Perimeter Institute in Canada, before hopping the pond and starting another three-year postdoc job in Denmark. With a grant from the EU, three years became four. More funding got me to five (with a fancier title), and now nearing on six. Each step, my contract has been temporary: at first three years at a time, then one-year extensions. Each year I applied, all over the world, looking for a permanent job: for a chance to settle down somewhere, to build my own research group without worrying about having to move the next year.

This year, things have finally worked out. In the Fall I will be moving to France, starting a junior permanent position with L’Institut de Physique Théorique (or IPhT) at CEA Paris-Saclay.

A photo of the entryway to the Institute, taken when I interviewed

It’s been a long journey to get here, with a lot of soul-searching. This year in particular has been a year of reassessment: of digging deep and figuring out what matters to me, what I hope to accomplish and what clues I have to guide the way. Sometimes I feel like I’ve matured more as a physicist in the last year than in the last three put together.

The CEA (originally Commissariat à l’énergie atomique, now Commissariat à l’énergie atomique et aux énergies alternatives, or Alternative Energies and Atomic Energy Commission, and yes that means they’re using the “A” for two things at the same time), is roughly a parallel organization to the USA’s Department of Energy. Both organizations began as a way to manage their nation’s nuclear program, but both branched out, both into other forms of energy and into scientific research. Both run a nationwide network of laboratories, lightly linked but independent from their nations’ universities, both with notable facilities for particle physics. The CEA’s flagship site is in Saclay, on the outskirts of Paris, and it’s their Institute for Theoretical Physics where I’ll be working.

My new position is genuinely permanent: unlike a tenure-track position in the US, I don’t go up for review after a fixed span of time, with the expectation that if I don’t get promoted I lose the job altogether. It’s also not a university, which in particular means I’m not required to teach. I’ll have the option of teaching, working with nearby universities. In the long run, I think I’ll pursue that option. I’ve found teaching helpful the past couple years: it’s helped me think about physics, and think about how to communicate physics. But it’s good not to have to rush into preparing a new course when I arrive, as new professors often do.

It’s also a really great group, with a lot of people who work on things I care about. IPhT has a long track record of research in scattering amplitudes, with many leading figures. They’ve played a key role in topics that frequent readers will have seen show up on this blog: on applying techniques from particle physics to gravitational waves, to the way Calabi-Yau manifolds show up in Feynman diagrams, and even recently to the relationship of machine learning to inference in particle physics.

Working temporary positions year after year, not knowing where I’ll be the next year, has been stressful. Others have had it worse, though. Some of you might have seen a recent post by Bret Deveraux, a military historian with a much more popular blog who has been in a series of adjunct positions. Deveraux describes the job market for the humanities in the US quite well. I’m in theoretical physics in Europe, so while my situation hasn’t been easy, it has been substantially better.

First, there’s the physics component. Physics has “adjunctified” much less than other fields. I don’t think I know a single physicist who has taken an adjunct teaching position, the kind of thing where you’re paid per course and only to teach. I know many who have left physics for other kinds of work, for Wall Street or Silicon Valley or to do data science for a bank or to teach high school. On the other side, I know people in other fields who do work as adjuncts, particularly in mathematics.

Deveraux blames the culture of his field, but I think funding also must have an important role. Physicists, and scientists in many other areas, rarely get professor positions right after their PhDs, but that doesn’t mean they leave the field entirely because most can find postdoc positions. Those postdocs are focused on research, and are often paid for by government grants: in my field in the US, that usually means the Department of Energy. People can go through two or sometimes even three such positions before finding something permanent, if they don’t leave the field before that. Without something like the Department of Energy or National Institutes of Health providing funding, I don’t know if the humanities could imitate that structure even if they wanted to.

Europe, in turn, has a different situation than the US. Most European countries don’t have a tenure-track: just permanent positions and fixed-term positions. Funding also works quite differently. Department of Energy funding in the US is spread widely and lightly: grants are shared by groups of theorists at a given university, each getting funding for a few postdocs and PhDs across the group. In Europe, a lot of the funding is much more concentrated: big grants from the European Research Council going to individual professors, with various national and private grants supplementing or mirroring that structure. That kind of funding, and the rarity of tenure, in turn leads to a different kind of temporary position: one not hired to teach a course but hired for research as long as the funding lasts. The Danish word for my current title is Adjunkt, but that’s as one says in France a faux ami: the official English translation is Assistant Professor, and it’s nothing like a US adjunct. I know people in a variety of forms of that kind of position in a variety of countries, people who landed a five-year grant where they could act like a professor, hire people and so on, but who in the end were expected to move when the grant was over. It’s a stressful situation, but at least it lets us further our research and make progress, unlike a US adjunct in the humanities or math who needs to spend much of their time on teaching.

I do hope Deveraux finds a permanent position, he’s got a great blog. And to return to the theme of the post, I am extremely grateful and happy that I have managed to find a permanent position. I’m looking forward to joining the group at Saclay: to learning more about physics from them, but also, to having a place where I can start to build something, and make a lasting impact on the world around me.

Extrapolated Knowledge

2 Replies

Scientists have famously bad work-life balance. You’ve probably heard stories of scientists working long into the night, taking work with them on weekends or vacation, or falling behind during maternity or paternity leave.

Some of this is culture. Certain fields have a very cutthroat attitude, with many groups competing to get ahead and careers on the line if they fail. Not every field is like that though: there are sub-fields that are more collaborative than competitive, that understand work-life balance and try to work together to a shared goal. I’m in a sub-field like that, so I know they exist.

Put aside the culture, and you’ve still got passion. Science is fun, it’s puzzle after puzzle, topics chosen because we find them fascinating. Even in the healthiest workplace you’d still have scientists pondering in the shower and scribbling notes on the plane, mixing business with pleasure because the work is genuinely both.

But there’s one more reason scientists are workaholics. I suspect, ultimately, it’s the most powerful reason. It’s that every scientist is, in some sense, irreplaceable.

In most jobs, if you go on vacation, someone can fill in when you’re gone. The replacement may not be perfect (think about how many times you watched movies in school with a substitute teacher), but they can cover for you, making some progress on your tasks until you get back. That works because you and they have a shared training, a common core that means they can step in and get what needs to be done done.

Scientists have shared training too, of course. Some of our tasks work the same way, the kind of thing that any appropriate expert can do, that just need someone to spend the time to do them.

But our training has a capstone, the PhD thesis. And the thing about a PhD thesis is that it is, always and without exception, original research. Each PhD thesis is an entirely new result, something no-one else had known before, discovered by the PhD candidate. Each PhD thesis is unique.

That, in turn, means that each scientist is unique. Each of us has our own knowledge, our own background, our own training, built up not just during the PhD but through our whole career. And sometimes, the work we do requires that unique background. It’s why we collaborate, why we reach out to different people around the world, looking for the unique few people who know how to do what we need.

Over time, we become a kind of embodiment of our accumulated knowledge. We build a perspective shaped by our experience, goals for the field and curiosity just a bit different from everyone else’s. We act as agents of that perspective, each the one person who can further our particular vision of where science is going. When we enter a collaboration, when we walk into the room at a conference, we are carrying with us all we picked up along the way, each a story just different enough to matter. We extrapolate from what we know, and try to do everything that knowledge can do.

So we can, and should, take vacations, yes, and we can, and should, try to maintain a work-life balance. We need to to survive, to stay sane. But we do have to accept that when we do, certain things won’t get done as fast. Our own personal vision, our extrapolated knowledge…will just have to wait.

Bottlenecks, Known and Unknown

Leave a reply

Scientists want to know everything, and we’ve been trying to get there since the dawn of science. So why aren’t we there yet? Why are there things we still don’t know?

Sometimes, the reason is obvious: we can’t do the experiments yet. Victorian London had neither the technology nor the wealth to build a machine like Fermilab, so they couldn’t discover the top quark. Even if Newton had the idea for General Relativity, the telescopes of the era wouldn’t have let astronomers see its effect on the motion of Mercury. As we grow (in technology, in resources, in knowledge, in raw number of human beings), we can test more things and learn more about the world.

But I’m a theoretical physicist, not an experimental physicist. I still want to understand the world, but what I contribute aren’t new experiments, but new ideas and new calculations. This brings back the question in a new form: why are there calculations we haven’t done yet? Why are there ideas we haven’t had yet?

Sometimes, we can track the reason down to bottlenecks. A bottleneck is a step in a calculation that, for some reason, is harder than the rest. As you try to push a calculation to new heights, the bottleneck is the first thing that slows you down, like the way liquid bubbles through the neck of a literal bottle. If you can clear the bottleneck, you can speed up your calculation and accomplish more.

In the clearest cases, we can see how these bottlenecks could be solved with more technology. As computers get faster and more powerful, calculations become possible that weren’t possible before, in the same way new experiments become possible with new equipment. This is essentially what has happened recently with machine learning, where relatively old ideas are finally feasible to apply on a massive scale.

In physics, a subtlety is that we rarely have access to the most powerful computers available. Some types of physics are done on genuine supercomputers, but for more speculative or lower-priority research we have to use small computer clusters, or even our laptops. Something can be a bottleneck not because it can’t be done on any computer, but because it can’t be done on the computers we can afford.

Most of the time, bottlenecks aren’t quite so obvious. That’s because in theoretical physics, often, we don’t know what we want to calculate. If we want to know why something happens, and not merely that it happens, then we need a calculation that we can interpret, that “makes sense” and that thus, hopefully, we can generalize. We might have some ideas for how that calculation could work: some property a mathematical theory might have that we already know how to understand. Some of those ideas are easy to check, so we check, and make progress. Others are harder, and we have to decide: is the calculation worth it, if we don’t know if it will give us the explanation we need?

Those decisions provide new bottlenecks, often hidden ones. As we get better at calculation, the threshold for an “easy” check gets easier and easier to meet. We put aside fewer possibilities, so we notice more things, which inspire yet more ideas. We make more progress, not because the old calculations were impossible, but because they weren’t easy enough, and now they are. Progress fuels progress, a virtuous cycle that gets us closer and closer to understanding everything we want to understand (which is everything).

Why Are Universities So International?

2 Replies

Worldwide, only about one in thirty people live in a different country from where they were born. Wander onto a university campus, though, and you may get a different impression. The bigger the university and the stronger its research, the more international its employees become. You’ll see international PhD students, international professors, and especially international temporary researchers like postdocs.

I’ve met quite a few people who are surprised by this. I hear the same question again and again, from curious Danes at outreach events to a tired border guard in the pre-clearance area of the Toronto airport: why are you, an American, working here?

It’s not, on the face of it, an unreasonable question. Moving internationally is hard and expensive. You may have to take your possessions across the ocean, learn new languages and customs, and navigate an unfamiliar bureaucracy. You begin as a temporary resident, not a citizen, with all the risks and uncertainty that involves. Given a choice, most people choose to stay close to home. Countries sometimes back up this choice with additional incentives. There are laws in many places that demand that, given a choice, companies hire a local instead of a foreigner. In some places these laws apply to universities as well. With all that weight, why do so many researchers move abroad?

Two different forces stir the pot, making universities international: specialization, and diversification.

Researchers may find it easier to live close to people who grew up with us, but we work better near people who share our research interests. Science, and scholarship more generally, are often collaborative: we need to discuss with and learn from others to make progress. That’s still very hard to do remotely: it requires serendipity, chance encounters in the corridor and chats at the lunch table. As researchers in general have become more specialized, we’ve gotten to the point where not just any university will do: the people who do our kind of work are few enough that we often have to go to other countries to find them.

Specialization alone would tend to lead to extreme clustering, with researchers in each area gathering in only a few places. Universities push back against this, though. A university wants to maximize the chance that one of their researchers makes a major breakthrough, so they don’t want to hire someone whose work will just be a copy of someone they already have. They want to encourage interdisciplinary collaboration, to try to get people in different areas to talk to each other. Finally, they want to offer a wide range of possible courses, to give the students (many of whom are still local), a chance to succeed at many different things. As a result, universities try to diversify their faculty, to hire people from areas that, while not too far for meaningful collaboration, are distinct from what their current employees are doing.

The result is a constant international churn. We search for jobs in a particular sweet spot: with people close enough to spur good discussion, but far enough to not overspecialize. That search takes us all over the world, and all but guarantees we won’t find a job where we were trained, let alone where we were born. It makes universities quite international places, with a core of local people augmented by opportune choices from around the world. It makes us, and the way we lead our lives, quite unusual on a global scale. But it keeps the science fresh, and the ideas moving.

Building the Railroad to Rigor

Leave a reply

As a kid who watched far too much educational television, I dimly remember learning about the USA’s first transcontinental railroad. Somehow, parts of the story stuck with me. Two companies built the railroad from different directions, one from California and the other from the middle of the country, aiming for a mountain in between. Despite the US Civil War happening around this time, the two companies built through, in the end racing to where the final tracks were laid with a golden spike.

I’m a theoretical physicist, so of course I don’t build railroads. Instead, I build new mathematical methods, ways to check our theories of particle physics faster and more efficiently. Still, something of that picture resonates with me.

You might think someone who develops new mathematical methods would be a mathematician, not a physicist. But while there are mathematicians who work on the problems I work on, their goals are a bit different. They care about rigor, about stating only things they can carefully prove. As such, they often need to work with simplified examples, “toy models” well-suited to the kinds of theorems they can build.

Physicists can be a bit messier. We don’t always insist on the same rigor the mathematicians do. This makes our results less reliable, but it makes our “toy models” a fair amount less “toy”. Our goal is to try to tackle questions closer to the actual real world.

What happens when physicists and mathematicians work on the same problem?

If the physicists worked alone, they might build and build, and end up with an answer that isn’t actually true. The mathematicians, keeping rigor in mind, would be safe in the truth of what they built, but might not end up anywhere near the physicists’ real-world goals.

Together, though, physicists and mathematicians can build towards each other. The physicists can keep their eyes on the mathematicians, correcting when they notice something might go wrong and building more and more rigor into their approach. The mathematicians can keep their eyes on the physicists, building more and more complex applications of their rigorous approaches to get closer and closer to the real world. Eventually, like the transcontinental railroad, the two groups meet: the mathematicians prove a rigorous version of the physicists’ approach, or the physicists adopt the mathematicians’ ideas and apply them to their own theories.

A sort of conference photo

In practice, it isn’t just two teams, physicists and mathematicians, building towards each other. Different physicists themselves work with different levels of rigor, aiming to understand different problems in different theories, and the mathematicians do the same. Each of us is building our own track, watching the other tracks build towards us on the horizon. Eventually, we’ll meet, and science will chug along over what we’ve built.

At Geometries and Special Functions for Physics and Mathematics in Bonn

Leave a reply

I’m at a workshop this week. It’s part of a series of “Bethe Forums”, cozy little conferences run by the Bethe Center for Theoretical Physics in Bonn.

You can tell it’s an institute for theoretical physics because they have one of these, but not a “doing room”

The workshop’s title, “Geometries and Special Functions for Physics and Mathematics”, covers a wide range of topics. There are talks on Calabi-Yau manifolds, elliptic (and hyper-elliptic) polylogarithms, and cluster algebras and cluster polylogarithms. Some of the talks are by mathematicians, others by physicists.

In addition to the talks, this conference added a fun innovative element, “my favorite problem sessions”. The idea is that a speaker spends fifteen minutes introducing their “favorite problem”, then the audience spends fifteen minutes discussing it. Some treated these sessions roughly like short talks describing their work, with the open directions at the end framed as their favorite problem. Others aimed broader, trying to describe a general problem and motivate interest in people of other sub-fields.

This was a particularly fun conference for me, because the seemingly distinct topics all connect in one way or another to my own favorite problem. In our “favorite theory” of N=4 super Yang-Mills, we can describe our calculations in terms of an “alphabet” of pieces that let us figure out predictions almost “by guesswork”. These alphabets, at least in the cases we know how to handle, turn out to correspond to mathematical structures called cluster algebras. If we look at interactions of six or seven particles, these cluster algebras are a powerful guide. For eight or nine, they still seem to matter, but are much harder to use.

For ten particles, though, things get stranger. That’s because ten particles is precisely where elliptic curves, and their related elliptic polylogarithms, show up. Things then get yet more strange, and with twelve particles or more we start seeing Calabi-Yau manifolds magically show up in our calculations.

We don’t know what an “alphabet” should look like for these Calabi-Yau manifolds (but I’m working on it). Because of that, we don’t know how these cluster algebras should appear.

In my view, any explanation for the role of cluster algebras in our calculations has to extend to these cases, to elliptic polylogarithms and Calabi-Yau manifolds. Without knowing how to frame an alphabet for these things, we won’t be able to solve the lingering mysteries that fill our field.

Because of that, “my favorite problem” is one of my biggest motivations, the question that drives a large chunk of what I do. It’s what’s made this conference so much fun, and so stimulating: almost every talk had something I wanted to learn.

All About the Collab

1 Reply

Sometimes, some scientists work alone. But mostly, scientists collaborate. We team up, getting more done together than we could alone.

Over the years, I’ve realized that theoretical physicists like me collaborate in a bit of a weird way, compared to other scientists. Most scientists do experiments, and those experiments require labs. Each lab typically has one principal investigator, or “PI”, who hires most of the other people in that lab. For any given project, scientists from the lab will be organized into particular roles. Some will be involved in the planning, some not. Some will do particular tests, gather data, manage lab animals, or do statistics. The whole experiment is at least roughly planned out from the beginning, and everyone has their own responsibility, to the extent that journals will sometimes ask scientists to list everyone’s roles when they publish papers. In this system, it’s rare for scientists from two different labs to collaborate. Usually it happens for a reason: a lab needs a statistician for a particularly subtle calculation, or one lab must process a sample so another lab can analyze it.

In contrast, theoretical physicists don’t have labs. Our collaborators sometimes come from the same university, but often they’re from a different one, frequently even in a different country. The way we collaborate is less like other scientists, and more like artists.

Sometimes, theoretical physicists have collaborations with dedicated roles and a detailed plan. This can happen when there is a specific calculation that needs to be done, that really needs to be done right. Some of the calculations that go into making predictions at the LHC are done in this way. I haven’t been in a collaboration like that (though in retrospect one collaborator may have had something like that in mind).

Instead, most of the collaborations I’ve been in have been more informal. They tend to start with a conversation. We chat by the coffee machine, or after a talk, anywhere there’s a blackboard nearby. It starts with “I’ve noticed something odd”, or “here’s something I don’t understand”. Then, we jam. We go back and forth, doing our thing and building on each other. Sometimes this happens in person, a barrage of questions and doubts until we hammer out something solid. Sometimes we go back to our offices, to calculate and look up references. Coming back the next day, we compare results: what did you manage to show? Did you get what I did? If not, why?

I make this sound spontaneous, but it isn’t completely. That starting conversation can be totally unplanned, but usually one of the scientists involved is trying to make it happen. There’s a different way you talk when you’re trying to start a collaboration, compared to when you just want to talk. If you’re looking for a collaboration, you go into more detail. If the other person is on the same wavelength, you start using “we” instead of “I”, or you start suggesting plans of action: “you could do X, while I do Y”. If you just want someone’s opinion, or just want to show off, then your conversation is less detailed, and less personal.

This is easiest to do with our co-workers, but we do it with people from other universities too. Sometimes this happens at conferences, more often during short visits for seminars. I’ve been on almost every end of this. As a visitor, I’ve arrived to find my hosts with a project in mind. As a host, I’ve invited a visitor with the goal of getting them involved in a collaboration, and I’ve received a visitor who came with their own collaboration idea.

After an initial flurry of work, we’ll have a rough idea of whether the project is viable. If it is, things get a bit more organized, and we sort out what needs to be done and a rough idea of who will do it. While the early stages really benefit from being done in person, this part is easier to do remotely. The calculations get longer but the concepts are clear, so each of us can work by ourselves, emailing when we make progress. If we get confused again, we can always schedule a Zoom to sort things out.

Once things are close (but often not quite done), it’s time to start writing the paper. In the past, I used Dropbox for this: my collaborators shared a folder with a draft, and we’d pass “control” back and forth as we wrote and edited. Now, I’m more likely to use something built for this purpose. Git is a tool used by programmers to collaborate on code. It lets you roll back edits you don’t like, and merge edits from two people to make sure they’re consistent. For other collaborations I use Overleaf, an online interface for the document-writing language LaTeX that lets multiple people edit in real-time. Either way, this part is also more or less organized, with a lot of “can you write this section?” that can shift around depending on how busy people end up being.

Finally, everything comes together. The edits stabilize, everyone agrees that the paper is good (or at least, that any dissatisfaction they have is too minor to be worth arguing over). We send it to a few trusted friends, then a few days later up on the arXiv it goes.

Then, the cycle begins again. If the ideas are still clear enough, the same collaboration might keep going, planning follow-up work and follow-up papers. We meet new people, or meet up with old ones, and establish new collaborations as we go. Our fortunes ebb and flow based on the conversations we have, the merits of our ideas and the strengths of our jams. Sometimes there’s more, sometimes less, but it keeps bubbling up if you let it.

Cabinet of Curiosities: The Train-Ladder

2 Replies

I’ve got a new paper out this week, with Andrew McLeod, Roger Morales, Matthias Wilhelm, and Chi Zhang. It’s yet another entry in this year’s “cabinet of curiosities”, quirky Feynman diagrams with interesting traits.

A while back, I talked about a set of Feynman diagrams I could compute with any number of “loops”, bypassing the approximations we usually need to use in particle physics. That wasn’t the first time someone did that. Back in the 90’s, some folks figured out how to do this for so-called “ladder” diagrams. These diagrams have two legs on one end for two particles coming in, two legs on the other end for two particles going out, and a ladder in between, like so:

There are infinitely many of these diagrams, but they’re all beautifully simple, variations on a theme that can be written down in a precise mathematical way.

Change things a little bit, though, and the situation gets wildly more intractable. Let the rungs of the ladder peek through the sides, and you get something looking more like the tracks for a train:

These traintrack integrals are much more complicated. Describing them requires the mathematics of Calabi-Yau manifolds, involving higher and higher dimensions as the tracks get longer. I don’t think there’s any hope of understanding these things for all loops, at least not any time soon.

What if we aimed somewhere in between? A ladder that just started to turn traintrack?

Add just a single pair of rungs, and it turns out that things remain relatively simple. If we do this, it turns out we don’t need any complicated Calabi-Yau manifolds. We just need the simplest Calabi-Yau manifold, called an elliptic curve. It’s actually the same curve for every version of the diagram. And the situation is simple enough that, with some extra cleverness, it looks like we’ve found a trick to calculate these diagrams to any number of loops we’d like.

(Another group figured out the curve, but not the calculation trick. They’ve solved different problems, though, studying all sorts of different traintrack diagrams. They sorted out some confusion I used to have about one of those diagrams, showing it actually behaves precisely the way we expected it to. All in all, it’s been a fun example of the way different scientists sometimes hone in on the same discovery.)

These developments are exciting, because Feynman diagrams with elliptic curves are still tough to deal with. We still have whole conferences about them. These new elliptic diagrams can be a long list of test cases, things we can experiment with with any number of loops. With time, we might truly understand them as well as the ladder diagrams!