Earlier this year, I made a list of topics I wanted to understand. The most abstract and technical of them was something called “Wilsonian effective field theory”. I still don’t understand Wilsonian effective field theory. But while thinking about it, I noticed something that seemed weird. It’s something I think many physicists already understand, but that hasn’t really sunk in with the public yet.
There’s an old problem in particle physics, described in many different ways over the years. Take our theories and try to calculate some reasonable number (say, the angle an electron turns in a magnetic field), and instead of that reasonable number we get infinity. We fix this problem with a process called renormalization that hides that infinity away, changing the “normalization” of some constant like a mass or a charge. While renormalization first seemed like a shady trick, physicists eventually understood it better. First, we thought of it as a way to work around our ignorance, that the true final theory would have no infinities at all. Later, physicists instead thought about renormalization in terms of scaling.
Imagine looking at the world on a camera screen. You can zoom in, or zoom out. The further you zoom out, the more details you’ll miss: they’re just too small to be visible on your screen. You can guess what they might be, but your picture will be different depending on how you zoom.
In particle physics, many of our theories are like that camera. They come with a choice of “zoom setting”, a minimum scale where they still effectively tell the whole story. We call theories like these effective field theories. Some physicists argue that these are all we can ever have: since our experiments are never perfect, there will always be a scale so small we have no evidence about it.
In general, theories can be quite different at different scales. Some theories, though, are especially nice: they look almost the same as we zoom in to smaller scales. The only things that change are the mass of different particles, and their charges.
One theory like this is Quantum Chromodynamics (or QCD), the theory of quarks and gluons. Zoom in, and the theory looks pretty much the same, with one crucial change: the force between particles get weaker. There’s a number, called the “coupling constant“, that describes how strong a force is, think of it as sort of like an electric charge. As you zoom in to quarks and gluons, you find you can still describe them with QCD, just with a smaller coupling constant. If you could zoom “all the way in”, the constant (and thus the force between particles) would be zero.
This makes QCD a rare kind of theory: one that could be complete to any scale. No matter how far you zoom in, QCD still “makes sense”. It never gives contradictions or nonsense results. That doesn’t mean it’s actually true: it interacts with other forces, like gravity, that don’t have complete theories, so it probably isn’t complete either. But if we didn’t have gravity or electricity or magnetism, if all we had were quarks and gluons, then QCD could have been the final theory that described them.
And this starts feeling a little weird, when you think about reductionism.
Philosophers define reductionism in many different ways. I won’t be that sophisticated. Instead, I’ll suggest the following naive definition: Reductionism is the claim that theories on larger scales reduce to theories on smaller scales.
Here “reduce to” is intentionally a bit vague. It might mean “are caused by” or “can be derived from” or “are explained by”. I’m gesturing at the sort of thing people mean when they say that biology reduces to chemistry, or chemistry to physics.
What happens when we think about QCD, with this intuition?
QCD on larger scales does indeed reduce to QCD on smaller scales. If you want to ask why QCD on some scale has some coupling constant, you can explain it by looking at the (smaller) QCD coupling constant on a smaller scale. If you have equations for QCD on a smaller scale, you can derive the right equations for a larger scale. In some sense, everything you observe in your larger-scale theory of QCD is caused by what happens in your smaller-scale theory of QCD.
But this isn’t quite the reductionism you’re used to. When we say biology reduces to chemistry, or chemistry reduces to physics, we’re thinking of just a few layers: one specific theory reduces to another specific theory. Here, we have an infinite number of layers, every point on the scale from large to small, each one explained by the next.
Maybe you think you can get out of this, by saying that everything should reduce to the smallest scale. But remember, the smaller the scale the smaller our “coupling constant”, and the weaker the forces between particles. At “the smallest scale”, the coupling constant is zero, and there is no force. It’s only when you put your hand on the zoom nob and start turning that the force starts to exist.
It’s reductionism, perhaps, but not as we know it.
Now that I understand this a bit better, I get some of the objections to my post about naturalness a while back. I was being too naive about this kind of thing, as some of the commenters (particularly Jacques Distler) noted. I believe there’s a way to rephrase the argument so that it still works, but I’d have to think harder about how.
I also get why I was uneasy about Sabine Hossenfelder’s FQXi essay on reductionism. She considered a more complicated case, where the chain from large to small scale could be broken, a more elaborate variant of a problem in Quantum Electrodynamics. But if I’m right here, then it’s not clear that scaling in effective field theories is even the right way to think about this. When you have an infinite series of theories that reduce to other theories, you’re pretty far removed from what most people mean by reductionism.
Finally, this is the clearest reason I can find why you can’t do science without an observer. The “zoom” is just a choice we scientists make, an arbitrary scale describing our ignorance. But without it, there’s no way to describe QCD. The notion of scale is an inherent and inextricable part of the theory, and it doesn’t have to mean our theory is incomplete.
Experts, please chime in here if I’m wrong on the physics here. As I mentioned at the beginning, I still don’t think I understand Wilsonian effective field theory. If I’m right though, this seems genuinely weird, and something more of the public should appreciate.

hi,
for those of us not in Particle Physics, it would be helpful to give an example or analogy for a case where the scale factor changes the physical effect of an interaction. As I see it, the familiar physical laws like electromagnetism are independent of scale : E = c q1 q2 /r as the electrostatic potential between two charges. The value of E changes as r changes, but the constant c does not change. So, this is not a good example of the effect you discuss. But what is?
What is the simplest case where renormalisation is required?
Is there an analogue in pure mathematics where a similar “technique” is used to get rid of infinities? Surely not the old L’Hopital’s rule?
LikeLike
This is a tricky question to answer, in part because some of what I’m talking about is genuinely a quantum effect. So it’s hard to find a physics analogy…but here’s a vaguer one:
Let’s say instead of physics, you’re studying international relations. You could think about different nations as having their own interests and desires, communicating and competing with each other. Alternatively, you could zoom in to a smaller scale, and look at the behavior of individual people. Once again, you’d model them with their own interests and desires, communicating and competing. Your models might look very similar, but some aspects would be different: maybe nations have more trouble communicating than people do, or have stronger “desires”. You’ve changed the scale and you’ve got almost the same theory, but a few of your “constants” have changed.
Quantum field theory is like that, but instead of just two “scales” it’s continuous. You need to do this in pretty much every quantum field theory. Only a few special ones have no infinities, and none of those are ones we use for everyday physics. Quantum electrodynamics, quantum chromodynamics, the Higgs boson, they all need renormalization.
There are lots of cases in mathematics where one regularizes to avoid infinities in one way or another. There are many different ways of doing this, depending on what you’re interested in doing. Here’s just one context.
LikeLike
I’d say that the scaling laws of classical materials can be considered a simpler example of this phenomenon. There is the classic fact, which I believe is due to Galileo, that if you have an object that’s a certain size you cannot scale all of its parts proportionally and expect this resized object to behave the same way. Compare a pillar in some cathedral that supports a certain weight, with its matching pillar in the doubled cathedral, which is twice as long and broad and must support a larger weight. If we imagine it is a square pillar then the doubled pillar can be thought of as being made of eight versions of the original pillar bunched together. Since placing one pillar on top of the other doesn’t affect how much weight it can support, the doubled pillar is equivalent to four of the original pillar placed side-by-side, and can support four times as much weight. On the other hand, the structure the doubled pillar is supporting can also be thought of as eight versions of the original structure, so has eight times the weight. So even if the original pillar can support its weight doesn’t mean that the pillar in the twice-as-large cathedral can.
To put it in a more idealized setting, if we consider a cube of some material with side-length L, and let be the its weight and
be the its weight and 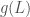 be the weight it can support, then
be the weight it can support, then 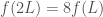 and
and  . More important than the actual formulas is how they are derived: By imagining a cube with side-length 2L as being made up of eight cubes with side-length L. In fact, for any length L’ much smaller than L we can model the cube of length L as being made up of many smaller cubes of length L’. The smaller L’ is, the better the model for the cube is, because it can account for things such the cube stretching and bending in a very detailed way or small pieces breaking off of it. However, for this to work the properties (strength weight, …) of the cube of length L’ need to be set to be compatible with the properties of the cube of length L.
. More important than the actual formulas is how they are derived: By imagining a cube with side-length 2L as being made up of eight cubes with side-length L. In fact, for any length L’ much smaller than L we can model the cube of length L as being made up of many smaller cubes of length L’. The smaller L’ is, the better the model for the cube is, because it can account for things such the cube stretching and bending in a very detailed way or small pieces breaking off of it. However, for this to work the properties (strength weight, …) of the cube of length L’ need to be set to be compatible with the properties of the cube of length L.
LikeLike
Pure speculattion, maybe (almost surelly wrong):
If really don’t have E=c q_1 q_2/r, but instead you have E=k q_1 q_2/(r^1.3), but you supposed it was like the first law and made an experiment with a typical scale L in which you measured “c”. Then, when you Made again your experiment ay different scales you saw that E≈c q_1 q_2/r -c ln(L’/L)q_1 q_2/r=(c-c ln(r/L)) q_1 q_2 as if your constant c wasn’t constant, but ir was something like c(r)≈c(L)-0.3 c(L) ln(r/L). The thing here is that your theory classically looks as if it behaved well only if you put the first thing, but then Quantum field theory rules moved your theory to behave un the second way.
LikeLike
This is kind of what’s going on, but there’s a key subtlety. In your example, the scientist doesn’t have to keep trying to measure “c”: if they’re smart enough they can figure out the real scaling and measure “k” instead.
The difference is that in quantum field theory, the equivalent “k” would have to be infinite. There just isn’t a “bare constant” that makes sense in theories like QCD. So the “c version” is our only choice in those cases.
LikeLike
I am not sure if it’s necesarelly Infinity. c and k have different scalling dimensions and c(lenght scale) will diverge if what’s really going on is k-like, but for knowing about k we need a nonperturbative definition on the theory, thing that we ussually don’t have.
In some CFT’s in two dimensions you know that you have that exactly.
I don’t know if that happens in QCD (I find really unlikely that it was the case, because of mass gap and that kind ir things). In N=4 is known what are the two point functions at nonperturbative level?
LikeLike
Ah sure. Yeah, if your theory is integrable or otherwise has a closed-form nonperturbative description then yeah, the analogy is much better. But indeed as you say QCD probably isn’t like that.
At least in planar N=4 the operator dimensions are known nonperturbatively yeah.
LikeLike
Water near the point of boiling. You have already small bubbles of vapor. The average size of these bubbles depends on temperature and increases if one comes close to the boiling temperature. The mathematics to handle this is the mathematics of renormalization.
The point of this type of renormalization is not to get rid of infinities. It is the atomic structure which regularizes the theory.
LikeLike
As a phenomenologist, this post sounds odd to me, because it seems to be conflating what could be consistent mathematically with what is true physically. Yes, it’s possible that QCD (or more realistically the SM) could be correct up to very high energy scales, in the sense that it wouldn’t be mathematically inconsistent.
But the point of parametrizing things with cutoff scales is that we don’t know if that actually is the case, in our universe! It is, after all, the point of science to figure out what actually exists. So the fact that QCD has a continuum limit and QED has a Landau pole just isn’t relevant from this point of view. We don’t care about extrapolating up to 10^100 TeV when qualitatively new stuff could appear at 10 TeV. The cutoff is meant to stand in for any number of unknown effects, which could range from just the same old boring scaling, to new particles, to even a breakdown of quantum field theory itself.
LikeLike
I agree, and I’m not saying that we should take QCD seriously as a theory to 10^100 TeV or whatever.
But some theory should be valid up to 10^100 TeV (even if all the theory says is “10^100 TeV doesn’t make sense”). It’s worth thinking about what sort of properties such a theory would need to have. And the impression I get (from people who seem to know Wilsonian EFT more than I do) is that one way such a theory could be is that it could be like QCD. That is, one type of theory that can be valid up to 10^100 TeV and beyond is an asymptotically free theory. Again, that doesn’t mean QCD itself is valid that far, just that when we do have a “final theory” it may well be asymptotically free (or I suppose asymptotically safe). Not the only option, but one of them.
And my point in this post is that’s weird! If the real world really was described by an asymptotically free theory up to arbitrarily high energies, that clashes with our naive intuitions about reductionism pretty heavily.
So does that mean the real world cannot be asymptotically free? I don’t think so, not on the basis of this at least. Does it mean our intuitions about reductionism are wrong? Probably! Does it mean quantum field theory itself is going to break down? Not because of this I don’t think, though it might break down anyway!
And yeah, it’s perfectly fine to approach all this by saying “we never have access to the far UV so who cares?” I don’t object to that attitude. But I think some people will still care, and it’s worth thinking about what to tell them.
LikeLike
I’m not sure there’s really any weirdness — there is no energy E at which a sufficiently precise experiment would be compatible with alpha_s(E) = 0. You’d always measure some deflection if you fired two quarks at one another from asymptotically far away (for example). Such an energy simply does not exist, given the input that alpha_s=4pi at some other energy. Thus, alpha_s always has somewhere to run from. Perhaps there’s an ambiguity about what “asymptotically far away” and “some deflection” mean in my sentence above, but those are IR questions, not UV ones, and those need to be dealt with to create a sensible S-matrix at any energy (which presumably, you’ve done if you’re talking about scattering and so forth)
LikeLike
I think that’s part of the weirdness though: yes, at any given energy, there’s a finite higher energy to run there from. The weirdness is that there’s no “final energy”, no lowest-level theory that your low-energy theories “reduce to”. It’s just an infinite (continuous) chain of one theory reducing to another. There’s nothing illogical or impossible about that, but it’s weird! I think it’s very much not something the average person would have expected to be possible.
LikeLike
Not trying to be obtuse, but: what is the alternative that you think is most satisfying? QED runs to a Landau pole, but maybe it’s just electronballs behaving like billiard balls at higher energy. Imagine QCD turning into nuclear physics (which itself is in some sense “residual” QCD forces between nucleons), just reversed as a function of energy — it doesn’t have to be something “heartier” like string theory (or the physics that underlies chemistry) up there to resolve the Landau pole. It might “just be”. This, too, is probably not “maximally classic reductionism,” but we don’t know which is the answer until we run an experiment at a sufficiently high energy. One case is equivalent to saying “there’s a few constants we can’t predict (like the electronball mass gap or electronball spectroscopic splittings),” while the other is saying “we were totally misled by what appeared to simple organizing principles at low energy, which have very different interpretations at high energies.”
Having a theory that is replaced (in a predictable way) by the same theory is a little simpler than either of these, but I think one way or another this points to the fact that there’s a continuum (or, if you prefer: “a wide range”) of possibility for UV completions. Perhaps this only reinforces your claim that the real picture is “very much not something the average person would have expected to be possible,” but I think you overestimate “what the average person would have expected to be possible” in the sense that the “average person” probably doesn’t even know that chemistry is derived from physics. I’d wager that understanding thermodynamic limits already puts someone in sufficiently rarefied company that they can accept that EFT is complicated 🙂
(As an unrelated quibble, let me say also that I think that your definition “Reductionism is the claim that theories on larger scales reduce to theories on smaller scales” uses “reduce to” in exactly the opposite way that most phenomenologists use it. To go to high energies is to “complete” the theory; to go to low energies is to “reduce” the theory. Think about the a- or c-theorems: the function monotonically decreases as energy decreases, which sounds like a reduction to me…)
LikeLike
There’s two uses of the word reduction that are clashing here, yes, and I’m leaning on the philosophical one (though I’ll admit I’ve never heard of going to the IR as “reducing” a theory, but maybe I just don’t talk to enough phenomenologists).
I think I see what you’re getting at here, but let me know if I’m misunderstanding. You’re saying that, if there are going to be some “physical accidents” in your theory anyway (value of the coupling, mass gaps, etc.) that can’t be explained by a more fundamental theory, then it shouldn’t really matter whether they’re continuously varying with scale (like QCD) or whether there is a final scale where they are defined (“electronballs”). Either way we have some high-energy theory that has unexplained properties.
In my view there is a meaningful difference, and it is that you can define your electronball theory without RG. That is, you can specify all the theory’s parameters without adding an artificial cutoff scale. The theory you get won’t necessarily be useful at all scales, but at least in principle physics at any scale would be derivable from a scale-agnostic theory.
That’s not true of QCD. You can’t define QCD without adding in a cutoff scale. If you don’t, you have no way of specifying the coupling. The theory depends on what is essentially a subjective quantity, the scale at which you choose to cut off your description.
I don’t blame you for being comfortable with that, I think as physicists have learned to accept it. But I think most people would find it strange, in the same way they find quantum mechanics strange. And I find it interesting that we don’t emphasize this when we talk about physics, in the same way we emphasize the weirdness of say quantum mechanics.
(As an aside: yes, the average person doesn’t care about physics at all. That’s a fully general argument against any point about “intuition” at all. For now, maybe it’s better to think about an “average reader of this blog”. I think my non-physicist readers would find this behavior of QCD interesting and weird, even if the literal average person wouldn’t.)
LikeLike
So, I guess where we part ways is the statement “you can define your electronball theory without RG” — why do you think that’s true? There are some (dimensionful) “high energy constants” in that theory, but there’s also running couplings that have threshold corrections and the whole works. The nuclear EFT, which can be defined at many scales (a “full” EFT, a pionless one, etc.), certainly has these properties (and they’re certainly not fully understood! RGEs in the nuclear EFT are an area of active research).
Perhaps QCD feels weird because, despite going to higher energies, the degrees of freedom remain the same — I think that’s ultimately the difference between QCD and electronball (or electronstring) theory: it just so happens that with QCD we’ve identified good degrees of freedom at what feels like a low scale. QED has a definite cutoff beyond which the degrees of freedom change to those of electronball/electronstring theory (whichever one is verified at the Nth collider after this one, I’m agnostic until then 🙂 ), but what that means to me is that when you say QCD “depends on what is essentially a subjective quantity, the scale at which you choose to cut off your description”, I’d say “so does QED” — you need to know how far you are from the Landau pole to know how good your calculation of electron scattering angles can possibly be, since there will be fractional corrections of order s/Lambda_Landau^2. This is why the prediction of the muon’s g-2 is less precise than the electron’s — schematically, alpha_EMalpha_sm_mu^2/Lambda_QCD^2 is a larger number than alpha_EMalpha_sm_e^2/Lambda_QCD^2, and hadronic matrix elements can’t be ignored in the muon calculation even though they can be in the electron one. If QCD-charged particles didn’t couple to the photon (say), then we would only have fractional uncertainties of order alpha_EMalpha_sm_mu^2/v_EW^2, which is quite a bit smaller. Ergo, the “scale at which you choose to cut off your description” matters here, too.
Let me say: I appreciate the back and forth, I’m glad you’re learning about EFT, and I’m by no means an expert in all this, so please keep at it if I’m being unclear or inconsistent!
LikeLike
Likewise, glad for the enlightening discussion!
I think in retrospect I was confused by whether in your last comment you were literally thinking of the electronballs behaving like (classical? quantum?) billiard balls, or whether you were thinking of a distinct QFT taking over there. Literal classical billiard balls can be certainly be defined without RG: you still might find RG useful for handling them, but you can specify all the “parameters of your theory” without it. I agree if you ended up with something more analogous to nuclear EFT then you likely can’t avoid RG, so my point is closer to “QFT is weird” than “specifically QCD is weird”. The latter just felt like a cleaner example.
That said, I think your argument about precision is missing the point. Yes, you don’t want to do perturbation theory in the bare coupling, even if you had one. That’s a good reason to use RG in practice. But when I pointed that out in a post explaining running couplings a while back, I got some (deserved!) pushback. RG isn’t just some pragmatic thing we do to make sure our perturbation theory works, in many cases it’s part of how the nonperturbative theory is defined. In the context of this post, the need to use RG to do perturbation theory isn’t particularly strange: you’re using something subjective (cutoff scale) to do something else subjective (get a good approximation under certain experimental conditions). What’s strange is if subjectivity is baked into the physics at its core, so that even if you could calculate everything exactly and nonperturbatively you’d need to add an arbitrary choice of scale.
LikeLike
Ah, sorry — by “like billiard balls” I just meant “without a long-range force.” But I didn’t mean for that to be taken too literally. Anything could happen above the Landau pole; we’d need to do experiments to figure out the right theory up there!
Anyway, I’m still not getting the point you’re trying to make. I simply don’t see a qualitative difference between QED/electronballology and QCD/nuclear physics. QED gives us an unambiguous Landau pole, QCD gives us an unambiguous strong coupling scale. The centrality of that energy doesn’t seem (to me) to be subjective in either theory. In some sense there’s a direction of RG flow that makes asymptotic freedom feel different, but in both cases there’s a strong coupling energy and simple prescription for what you do away from that energy.
LikeLike
There’s a particular loophole I was worried about that it sounds like you might be invoking, so to clarify: are you saying that once you specify the strong-coupling scale, QCD is unambiguous? I.E., there are no other free parameters, and the only difference between QCD with different couplings is the choice of units you use for energy?
If that’s the case, I agree that my argument doesn’t work. If it is, is the same true for QCD with massive quarks? I would think that at some point you’d need to consider a theory with multiple scales and there would be a free parameter that wouldn’t just come down to a choice of units.
If that’s not what you were getting at (or in a sufficiently complicated theory if QCD doesn’t work for this), then I’d argue that the direction of the flow actually does matter, at least if we still care about philosophical reductionism. If we do, then we expect parameters at low energy to be determined by parameters at high energy, and not the reverse. Even if we can do the math either way, one direction has a causal meaning that the other doesn’t.
Again, this may well mean we shouldn’t care about philosophical reductionism. It also may just mean, as I comment in the post, that it’s wrong to think about EFT in terms of low-energy scale EFTs philosophically reducing to high-energy scale EFTs, and that really we should be thinking of reductionism in terms of non-QFT theories reducing to QFT, and not of different scales of the same EFT reducing to each other.
LikeLike
To answer the question as cleanly as possible (and according to my best understanding, which, again, may not be perfect): once you specify Lambda_QCD and the numbers and masses of quarks*, then QCD is unique. It just so happens that QCD appears “simple” at energies above strong coupling and QED appears “simple” at energies below; the “aboveness or belowness” is determined by the gauge group and matter content, but each is unique, and (to me) neither is weirder or less scale-sensitive than the other. Interestingly, going to more supersymmetric QFTs typically allows one to formulate a duality between theories with different matter and gauge content such that there’s a “simple” calculation at any scale (one theory is weakly coupled when the other is strongly coupled) — this, I think, is where some of the truest “weirdness” (or beauty) of QFT lurks 🙂
*you need to know the masses to know when to add threshold corrections and alter the running
LikeLike
Hmm. Ok, so is one way to think about this that a theory is defined by the shape of its RG trajectories? So I draw some curve for the behavior of the coupling, it diverges at some point and its running changes at other points, and the ratio between the point where it diverges and the point its running changes is the ratio between Lambda_QCD and one of the quark masses?
I think that works from one of the perspectives I was describing: if you call QCD itself a “theory”, then you’re fine: you have a well-defined theory, and theories at lower energies (pion models, chemistry…) (philosophically) reduce to that theory.
It’s still confusing from the other perspective, where the individual theories are things like “QCD at scale 1 TeV” instead of “QCD as a whole”. From that perspective, you ask “why does the coupling diverge at Lambda_QCD?” and the answer is “because the coupling was X at Y energy above Lambda_QCD”, and you get the weird infinite regress of “why X? Because Y” that was bugging me earlier. (Again, maybe that means this perspective is just wrong!)
Overall, there’s something deeper that bugs me, which is the statement that you need RG to define (not just use in practice, but define) any of these theories in the first place. But maybe I’m mistaken about that, and you can imagine one of these theories just defined by all its correlation functions with no mention of RG?
I agree that there’s a lot of weirdness once duality enters the picture, but on a certain level (at least from my perspective), it’s not as weird, because the theories related are usually CFTs, or otherwise theories without UV divergences (and often, integrable theories). So you’ve got two perspectives, one where the coupling is strong and the other where it is weak, but ultimately you can think about the theory as defined by correlation functions with some parameters, and the duality just corresponding to how you interpret the “meaning” of those parameters and correlation functions.
LikeLike
I think I’d agree that “a theory is defined by the shape of its RG trajectories,” but if you want to literally define a theory which is “QCD at scale 1 TeV” instead of “QCD as a whole”, then you are no longer allowed to ask “why does the coupling diverge at Lambda_QCD?” — you only have one energy, which is 1 TeV. The coupling is well-defined for this “candidate theory,” but you can’t access Lambda_QCD. Only “QCD as a whole” allows you to run between energies and ask questions about different energies
As for “Overall, there’s something deeper that bugs me, which is the statement that you need RG to define (not just use in practice, but define) any of these theories in the first place. But maybe I’m mistaken about that, and you can imagine one of these theories just defined by all its correlation functions with no mention of RG?” — I’ll hazard that an alternate “complete” definition of a theory is via its correlation functions as well as every operator’s (exact) scaling dimension (which in a weakly coupled limit tells you how it behaves under RG evolution), but now I’m really out of my element 🙂
LikeLike
Wouldn’t you still be able to access Lambda_QCD from the “QCD at scale 1 TeV” theory, though? The higher-energy theories on the trajectory should have all the information about what happens at lower energies (barring a version of a Landau pole that presents an essential singularity like Hossenfelder was speculating about).
Fair enough about correlation functions+scaling dimensions. In CFT indeed all you need is the dimension of each operator and the structure constants (both as exact functions of the coupling). But I had the impression that there’s an issue with this for non-CFTs. I’m out of my element there too so I may just be misremembering!
LikeLike
I was just being pedantic about accessing Lambda_QCD from 1 TeV — if you define a theory in which sqrt(s) = 10 TeV but all other facts about QCD obtain, then, well: this is a theory where sqrt(s) is always 10 TeV. You can change the number of incoming states that you prepare when you run an experiment, perhaps, and you can speculate about an alternate universe where sqrt(s) sometimes reaches as low as Lambda_QCD, but sqrt(s) for you is always 10 TeV, so you’ll never test those speculations. But, yes, you’d get the right energy scale when you (and your 10 TeV pencil) did the calculation 🙂
LikeLike
Ok, now I’m confused. I had the impression that the “scale” of a theory wasn’t literally sqrt(s) (after all, if you aren’t computing a scattering amplitude you don’t even have an “s”!) Rather, it was a cutoff scale that characterizes how you’ve coarse-grained. Calculating things at other energies will introduce large logarithms and make your perturbation theory worse, but the theory isn’t inapplicable at those energies, it’s just less useful. Am I mistaken?
LikeLike
Ah — I misunderstood. Yes, what you’ve written is correct: there are higher-twist operators and so forth which would seem to blow up beyond X TeV, but which you can calculate with at any energy below X TeV. I thought you were describing something narrower — indeed, you’re using totally standard terminology, I just misinterpreted. Carry on 🙂
LikeLike
I’m not sure that I buy your line of reasoning in the case of QCD.
Generally speaking, the theory that most people would think about reducing to QCD would be effective theories of nuclear physics involving atoms made up of multiple nucleons.
In theory, you can explain the behavior of these atoms predominantly with QCD from first principles, with a little sprinkling of electroweak theory. But, in practice, we have a hard enough time explaining the behavior of single hadrons or two to four hadrons with QCD from first principles without resorting to numerical or analytical approximations because the math involved in QCD is so hard (in part because it is a strong non-abelian force in which gluons interact with each other, unlike photons which carry an abelian force without self-interactions and the weak force that usually gets summarized as a black box set of input-output matrixes).
So, instead we resort to a phenomenological residual nuclear force inspired by our qualitative understanding of QCD to understand bigger atoms (hadrons compounds made of hadron other than nucleons don’t seem to be observed at scales large than meson and baryon molecules with a couple of hadrons in a non-confined system anyway, and quark-gluon plasma can be thought of a single special case with the mix of quarks in it and the temperature as parameters for that special case). At the most basic level, the phenomenology is done crudely by estimating based upon measured atomic isotope masses the nuclear binding energy in an atomic isotope to determine the exothermic or endothermic properties of possible nuclear fusion and nuclear fission reactions involve them. At a more advanced level, we model it as one or several Yukawa forces mediated by several massive but light mesons, but mostly by pions.
Likewise, at the next discrete level, we then turn to chemistry and condensed matter physics, which is dominated by underlying QED interactions, to understand molecules and ionic compounds, as opposed to single atoms, since the residual nuclear force and weak force are rarely important in understanding chemistry and condensed matter physics at this scale.
In basic structure (e.g. in path integrals and boson propagators), QED and QCD are very similar, except for the self-interaction terms and the fact that the QCD infinite series require far more terms than the parallel infinite series in QED, to produce meaningful results. So, I’m a bit puzzled while QED or weak force theory would be singled out in the same way as a mere effective field theory relative to QCD.
Also, while QCD is, in theory, generalizable up to arbitrary scales, in practice, the twin boundaries of confinement and asymptotic freedom, tightly defines the scale at which it applies in the context of the fundamental masses (subject to only modest renormalization in most circumstances) of the hadronizing quarks (i.e. u, d, s, c and b), with confinement preventing pure, direct gluon-quark interactions between hadrons from being important, and asymptotic freedom preventing very small distance QCD interactions from being very interesting.
Further, above the roughly 1 GeV temperature scale, you get a phase shift into quark-gluon plasma and a discrete change in the effective phenomenological outcome into the QGP special case with one vector parameter representing the relative proportions of different quark types and one scalar parameter representing temperature, as a very precise first order approximation.
It is still stunning how much structure can arise from the naively very simple rules of QCD and its modest number of experimentally determined parameters. But, I also don’t know how much time I’ve squandered puzzling over why it is that the universe has scores of hadrons and hadron molecules, that somehow end up boiling down to two kinds of baryons (the proton and the neutron), and a few light mesons to carry the residual nuclear force, for all but the first few moments after the big bang, and some isolated and sporadic interactions that take mere moments in the history of the universe in particle colliders and perhaps in supernovae, in and around black holes, neutron stars and perhaps a few other hypothetic stellar creatures like quark stars. How did we end up with a universe that gets so little mileage out of such a simple yet rich fundamental theory like QCD?
LikeLike
Actually deriving the full behavior of a theory on large scales from its small-scale properties is almost always out of reach, and QCD is indeed no exception. What’s bothering me in this post is less what we can calculate in practice, and more what our theories determine in principle. If the world was QCD, what would that mean? Is QCD the kind of thing the world can be?
And with that in mind, it bothers me that once we get down to our supposedly most fundamental theory, it’s not actually one theory. It’s a series of theories, each one at a different scale, stretching off to the (infinite) limit of asymptotic freedom. And it’s not clear that we can define it in any other way, not just in practice but perhaps in principle. That’s weird!
(By the way, I think you’re conflating “QCD becomes QGP at high energies” with “QCD isn’t described by field theory at high energies”. QCD collectively behaves as QGP at high energies, but an individual quark inside QGP is basically as close to nice perturbative QCD behavior as you can get.)
LikeLike