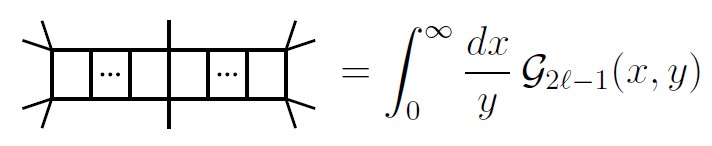Tag Archives: DoingScience

Cabinet of Curiosities: The Train-Ladder

2 Replies

I’ve got a new paper out this week, with Andrew McLeod, Roger Morales, Matthias Wilhelm, and Chi Zhang. It’s yet another entry in this year’s “cabinet of curiosities”, quirky Feynman diagrams with interesting traits.

A while back, I talked about a set of Feynman diagrams I could compute with any number of “loops”, bypassing the approximations we usually need to use in particle physics. That wasn’t the first time someone did that. Back in the 90’s, some folks figured out how to do this for so-called “ladder” diagrams. These diagrams have two legs on one end for two particles coming in, two legs on the other end for two particles going out, and a ladder in between, like so:

There are infinitely many of these diagrams, but they’re all beautifully simple, variations on a theme that can be written down in a precise mathematical way.

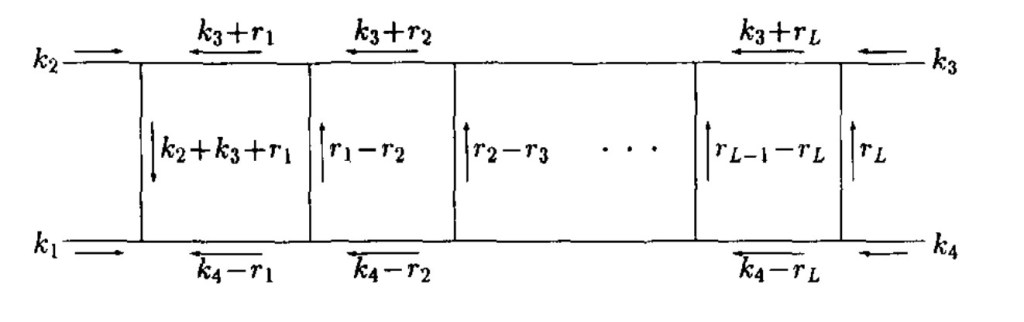
Change things a little bit, though, and the situation gets wildly more intractable. Let the rungs of the ladder peek through the sides, and you get something looking more like the tracks for a train:

These traintrack integrals are much more complicated. Describing them requires the mathematics of Calabi-Yau manifolds, involving higher and higher dimensions as the tracks get longer. I don’t think there’s any hope of understanding these things for all loops, at least not any time soon.

What if we aimed somewhere in between? A ladder that just started to turn traintrack?

Add just a single pair of rungs, and it turns out that things remain relatively simple. If we do this, it turns out we don’t need any complicated Calabi-Yau manifolds. We just need the simplest Calabi-Yau manifold, called an elliptic curve. It’s actually the same curve for every version of the diagram. And the situation is simple enough that, with some extra cleverness, it looks like we’ve found a trick to calculate these diagrams to any number of loops we’d like.

(Another group figured out the curve, but not the calculation trick. They’ve solved different problems, though, studying all sorts of different traintrack diagrams. They sorted out some confusion I used to have about one of those diagrams, showing it actually behaves precisely the way we expected it to. All in all, it’s been a fun example of the way different scientists sometimes hone in on the same discovery.)

These developments are exciting, because Feynman diagrams with elliptic curves are still tough to deal with. We still have whole conferences about them. These new elliptic diagrams can be a long list of test cases, things we can experiment with with any number of loops. With time, we might truly understand them as well as the ladder diagrams!

The Many Varieties of Journal Club

Leave a reply

Across disciplines, one tradition seems to unite all academics: the journal club. In a journal club, we gather together to discuss papers in academic journals. Typically, one person reads the paper in depth in advance, and comes prepared with a short presentation, then everyone else asks questions. Everywhere I’ve worked has either had, or aspired to have, a journal club, and every academic I’ve talked to recognizes the concept.

Beyond that universal skeleton, though, are a lot of variable details. Each place seems to interpret journal clubs just a bit differently. Sometimes a lot differently.

For example, who participates in journal clubs? In some places, journal clubs are a student thing, organized by PhD or Master’s students to get more experience with their new field. Some even have journal clubs as formal courses, for credit and everything. In other places, journal clubs are for everyone, from students up through the older professors.

What kind of papers? Some read old classic papers, knowing that without an excuse we’d never take the time to read them and would miss valuable insights. Some instead focus on the latest results, as a way to keep up with progress in the field.

Some variation is less intentional. Academics are busy, so it can be hard to find a volunteer to prepare a presentation on a paper every week. This leads journal clubs to cut corners, in once again a variety of ways. A journal club focused on the latest papers can sometimes only find volunteers interested in presenting their own work (which we usually already have a presentation prepared for). Sometimes this goes a step further, and the journal club becomes a kind of weekly seminar: a venue for younger visitors to talk about their work that’s less formal than a normal talk. Sometimes, instead of topic, the corner cut is preparation: people still discuss new papers, but instead of preparing a presentation they just come and discuss on the fly. This gets dangerous, because after a certain point people may stop reading the papers altogether, hoping that someone else will come having read it to explain it!

Journal clubs are tricky. Academics are curious, but we’re also busy and lazy. We know it would be good for us to discuss, to keep up with new papers or read the old classics… but actually getting organized, that’s another matter!

When Your Research Is a Cool Toy

1 Reply

Merry Newtonmas, everyone!

In the US, PhD students start without an advisor. As they finish their courses, different research groups make their pitch, trying to get them to join. Some promise interesting puzzles and engaging mysteries, others talk about the importance of their work, how it can help society or understand the universe.

Thinking back to my PhD, there is one pitch I remember to this day. The pitch was from the computational astrophysics group, and the message was a simple one: “we blow up stars”.

Obviously, these guys didn’t literally blow up stars: they simulated supernovas. They weren’t trying to make some weird metaphysical argument, they didn’t believe their simulation was somehow the real thing. The point they were making, instead, was emotional: blowing up stars feels cool.

Scientists can be motivated by curiosity, fame, or altruism, and these are familiar things. But an equally important motivation is a sense of play. If your job is to build tiny cars for rats, some of your motivation has to be the sheer joy of building tiny cars for rats. If you simulate supernovas, then part of your motivation can be the same as my nephew hurling stuffed animals down the stairs: that joyful moment when you yell “kaboom!”

Probably, your motivation shouldn’t just be to play with a cool toy. You need some of those “serious” scientific motivations as well. But for those of you blessed with a job where you get to say “kaboom”, you have that extra powerful reason to get up in the morning. And for those of you just starting a scientific career, may you have some cool toys under your Newtonmas tree!

This Week at Quanta Magazine

3 Replies

I’ve got an article in Quanta Magazine this week, about a program called FORM.

Quanta has come up a number of times on this blog, they’re a science news outlet set up by the Simons Foundation. Their goal is to enhance the public understanding of science and mathematics. They cover topics other outlets might find too challenging, and they cover the topics others cover with more depth. Most people I know who’ve worked with them have been impressed by their thoroughness: they take fact-checking to a level I haven’t seen with other science journalists. If you’re doing a certain kind of mathematical work, then you hope that Quanta decides to cover it.

A while back, as I was chatting with one of their journalists, I had a startling realization: if I want Quanta to cover something, I can send them a tip, and if they’re interested they’ll write about it. That realization resulted in the article I talked about here. Chatting with the journalist interviewing me for that article, though, I learned something if anything even more startling: if I want Quanta to cover something, and I want to write about it, I can pitch the article to Quanta, and if they’re interested they’ll pay me to write about it.

Around the same time, I happened to talk to a few people in my field, who had a problem they thought Quanta should cover. A software, called FORM, was used in all the most serious collider physics calculations. Despite that, the software wasn’t being supported: its future was unclear. You can read the article to learn more.

One thing I didn’t mention in that article: I hadn’t used FORM before I started writing it. I don’t do those “most serious collider physics calculations”, so I’d never bothered to learn FORM. I mostly use Mathematica, a common choice among physicists who want something easy to learn, even if it’s not the strongest option for many things.

(By the way, it was surprisingly hard to find quotes about FORM that didn’t compare it specifically to Mathematica. In the end I think I included one, but believe me, there could have been a lot more.)

Now, I wonder if I should have been using FORM all along. Many times I’ve pushed to the limits of what Mathematica could comfortable handle, the limits of what my computer’s memory could hold, equations long enough that just expanding them out took complicated work-arounds. If I had learned FORM, maybe I would have breezed through those calculations, and pushed even further.

I’d love it if this article gets FORM more attention, and more support. But also, I’d love it if it gives a window on the nuts and bolts of hard-core particle physics: the things people have to do to turn those T-shirt equations into predictions for actual colliders. It’s a world in between physics and computer science and mathematics, a big part of the infrastructure of how we know what we know that, precisely because it’s infrastructure, often ends up falling through the cracks.

Edit: For researchers interested in learning more about FORM, the workshop I mentioned at the end of the article is now online, with registrations open.

Confidence and Friendliness in Science

6 Replies

I’ve seen three kinds of scientific cultures.

First, there are folks who are positive about almost everyone. Ask them about someone else’s lab, even a competitor, and they’ll be polite at worst, and often downright excited. Anyone they know, they’ll tell you how cool the work they’re doing is, how it’s important and valuable and worth doing. They might tell you they prefer a different approach, but they’ll almost never bash someone’s work.

I’ve heard this comes out of American culture, and I can kind of see it. There’s an attitude in the US that everything needs to be described as positively as possible. This is especially true in a work context. Negativity is essentially a death sentence, doled out extremely rarely: if you explicitly say someone or their work is bad, you’re trying to get them fired. You don’t do that unless someone really really deserves it.

That style of scientific culture is growing, but it isn’t universal. There’s still a big cultural group that is totally ok with negativity: as long as it’s directed at other people, anyway.

This scientific culture prides itself on “telling it like it is”. They’ll happily tell you about how everything everyone else is doing is bullshit. Sometimes, they claim their ideas are the only ways forward. Others will have a small number of other people who they trust, who have gained their respect in one way or another. This sort of culture is most stereotypically associated with Russians: a “Russian-style” seminar, for example, is one where the speaker is aggressively questioned for hours.

It may sound like those are the only two options, but there is a third. While “American-style” scientists don’t criticize anyone, and “Russian-style” scientists criticize everyone else, there are also scientists who criticize almost everyone, including themselves.

With a light touch, this culture can be one of the best. There can be a real focus on “epistemic humility”, on always being clear of how much we still don’t know.

However, it can be worryingly easy to spill past that light touch, into something toxic. When the criticism goes past humility and into a lack of confidence in your own work, you risk falling into a black hole, where nothing is going well and nobody has a way out. This kind of culture can spread, filling a workplace and infecting anyone who spends too long there with the conviction that nothing will ever measure up again.

If you can’t manage that light skeptical touch, then your options are American-style or Russian-style. I don’t think either is obviously better. Both have their blind spots: the Americans can let bad ideas slide to avoid rocking the boat, while the Russians can be blind to their own flaws, confident that because everyone else seems wrong they don’t need to challenge their own worldview.

You have one more option, though. Now that you know this, you can recognize each for what it is: not the one true view of the world, but just one culture’s approach to the truth. If you can do that, you can pick up each culture as you need, switching between them as you meet different communities and encounter different things. If you stay aware, you can avoid fighting over culture and discourse, and use your energy on what matters: the science.

Visiting the IAS

Leave a reply

I’m at the Institute for Advanced Study, or IAS, this week.

There isn’t a conference going on, but if you looked at the visitor list you’d be forgiven for thinking there was. We have talks in my subfield almost every day this week, two professors from my subfield here on sabbatical, and extra visitors on top of that.

The IAS is a bit of an odd place. Partly, that’s due to its physical isolation: tucked away in the woods behind Princeton, a half-hour’s walk from the nearest restaurant, it’s supposed to be a place for contemplation away from the hustle and bustle of the world.

Since the last time I visited they’ve added a futuristic new building, seen here out of my office window. The building is most notable for one wild promise: someday, they will serve dinner there.

Mostly, though, the weirdness of the IAS is due to the kind of institution it is.

Within a given country, most universities are pretty similar. Each may emphasize different teaching styles, and the US has a distinction between public and private, but (neglecting scammy for-profit universities), there are some commonalities of structure: both how they’re organized, and how they’re funded. Even between countries, different university systems have quite a bit of overlap.

The IAS, though, is not a university. It’s an independent institute. Neighboring Princeton supplies it with PhD students, but otherwise the IAS runs, and funds, itself.

There are a few other places like that around the world. The Perimeter Institute in Canada is also independent, and also borrows students from a neighboring university. CERN pools resources from several countries across Europe and beyond, Nordita from just the Nordic countries. Generalizing further, many countries have some sort of national labs or other nation-wide systems, from US Department of Energy labs like SLAC to Germany’s Max Planck Institutes.

And while universities share a lot in common, non-university institutes can be very different. Some are closely tied to a university, located inside university buildings with members with university affiliations. Others sit at a greater remove, less linked to a university or not linked at all. Some have their own funding, investments or endowments or donations, while others are mostly funded by governments, or groups of governments. I’ve heard that the IAS gets about 10% of its budget from the government, while Perimeter gets its everyday operating expenses entirely from the Canadian government and uses donations for infrastructure and the like.

So ultimately, the IAS is weird because every organization like it is weird. There are a few templates, and systems, but by and large each independent research organization is different. Understanding one doesn’t necessarily help at understanding another.

Fields and Scale

3 Replies

I am a theoretical particle physicist, and every morning I check the arXiv.

arXiv.org is a type of website called a preprint server. It’s where we post papers before they are submitted to (and printed by) a journal. In practice, everything in our field shows up on arXiv, publicly accessible, before it appears anywhere else. There’s no peer review process on arXiv, the journals still handle that, but in our field peer review doesn’t often notice substantive errors. So in practice, we almost never read the journals: we just check arXiv.

And so every day, I check the arXiv. I go to the section on my sub-field, and I click on a link that lists all of the papers that were new that day. I skim the titles, and if I see an interesting paper I’ll read the abstract, and maybe download the full thing. Checking as I’m writing this, there were ten papers posted in my field, and another twenty “cross-lists” were posted in other fields but additionally classified in mine.

Other fields use arXiv: mathematicians and computer scientists and even economists use it in roughly the same way physicists do. For biology and medicine, though, there are different, newer sites: bioRxiv and medRxiv.

One thing you may notice is the different capitalization. When physicists write arXiv, the “X” is capitalized. In the logo, it looks like a Greek letter chi, thus saying “archive”. The biologists and medical researchers capitalize the R instead. The logo still has an X that looks like a chi, but positioned with the R it looks like the Rx of medical prescriptions.

Something I noticed, but you might not, was the lack of a handy link to see new papers. You can search medRxiv and bioRxiv, and filter by date. But there’s no link that directly takes you to the newest papers. That suggests that biologists aren’t using bioRxiv like we use arXiv, and checking the new papers every day.

I was curious if this had to do with the scale of the field. I have the impression that physics and mathematics are smaller fields than biology, and that much less physics and mathematics research goes on than medical research. Certainly, theoretical particle physics is a small field. So I might have expected arXiv to be smaller than bioRxiv and medRxiv, and I certainly would expect fewer papers in my sub-field than papers in a medium-sized subfield of biology.

On the other hand, arXiv in my field is universal. In biology, bioRxiv and medRxiv are still quite controversial. More and more people are using them, but not every journal accepts papers posted to a preprint server. Many people still don’t use these services. So I might have expected bioRxiv and medRxiv to be smaller.

Checking now, neither answer is quite right. I looked between November 1 and November 2, and asked each site how many papers were uploaded between those dates. arXiv had the most, 604 papers. bioRxiv had roughly half that many, 348. medRxiv had 97.

arXiv represents multiple fields, bioRxiv is “just” biology. Specializing, on that day arXiv had 235 physics papers, 135 mathematics papers, and 250 computer science papers. So each individual field has fewer papers than biology in this period.

Specializing even further, I can look at a subfield. My subfield, which is fairly small, had 20 papers between those dates. Cell biology, which I would expect to be quite a big subfield, had 33.

Overall, the numbers were weirdly comparable, with medRxiv unexpectedly small compared to both arXiv and bioRxiv. I’m not sure whether there are more biologists than physicists, but I’m pretty sure there should be more cell biologists than theoretical particle physicists. This suggests that many still aren’t using bioRxiv. It makes me wonder: will bioRxiv grow dramatically in future? Are the people running it ready for if it does?

From Journal to Classroom

6 Replies

As part of the pedagogy course I’ve been taking, I’m doing a few guest lectures in various courses. I’ve got one coming up in a classical mechanics course (“intermediate”-level, so not Newton’s laws, but stuff the general public doesn’t know much about like Hamiltonians). They’ve been speeding through the core content, so I got to cover a “fun” topic, and after thinking back to my grad school days I chose a topic I think they’ll have a lot of fun with: Chaos theory.

Getting the obligatory Warhammer reference out of the way now

Chaos is one of those things everyone has a vague idea about. People have heard stories where a butterfly flaps its wings and causes a hurricane. Maybe they’ve heard of the rough concept, determinism with strong dependence on the initial conditions, so a tiny change (like that butterfly) can have huge consequences. Maybe they’ve seen pictures of fractals, and got the idea these are somehow related.

Its role in physics is a bit more detailed. It’s one of those concepts that “intermediate classical mechanics” is good for, one that can be much better understood once you’ve been introduced to some of the nineteenth century’s mathematical tools. It felt like a good way to show this class that the things they’ve learned aren’t just useful for dusty old problems, but for understanding something the public thinks is sexy and mysterious.

As luck would have it, the venerable textbook the students are using includes a (2000’s era) chapter on chaos. I read through it, and it struck me that it’s a very different chapter from most of the others. This hit me particularly when I noticed a section describing a famous early study of chaos, and I realized that all the illustrations were based on the actual original journal article.

I had surprisingly mixed feelings about this.

On the one hand, there’s a big fashion right now for something called research-based teaching. That doesn’t mean “using teaching methods that are justified by research” (though you’re supposed to do that too), but rather, “tying your teaching to current scientific research”. This is a fashion that makes sense, because learning about cutting-edge research in an undergraduate classroom feels pretty cool. It lets students feel more connected with the scientific community, it inspires them to get involved, and it gets them more used to what “real research” looks like.

On the other hand, structuring your textbook based on the original research papers feels kind of lazy. There’s a reason we don’t teach Newtonian mechanics the way Newton would have. Pedagogy is supposed to be something we improve at over time: we come up with better examples and better notation, more focused explanations that teach what we want students to learn. If we just summarize a paper, we’re not really providing “added value”: we should hope, at this point, that we can do better.

Thinking about this, I think the distinction boils down to why you’re teaching the material in the first place.

With a lot of research-based teaching, the goal is to show the students how to interact with current literature. You want to show them journal papers, not because the papers are the best way to teach a concept or skill, but because reading those papers is one of the skills you want to teach.

That makes sense for very current topics, but it seems a bit weird for the example I’ve been looking at, an early study of chaos from the 60’s. It’s great if students can read current papers, but they don’t necessarily need to read older ones. (At least, not yet.)

What then, is the textbook trying to teach? Here things get a bit messy. For a relatively old topic, you’d ideally want to teach not just a vague impression of what was discovered, but concrete skills. Here though, those skills are just a bit beyond the students’ reach: chaos is more approachable than you’d think, but still not 100% something the students can work with. Instead they’re learning to appreciate concepts. This can be quite valuable, but it doesn’t give the kind of structure that a concrete skill does. In particular, it makes it hard to know what to emphasize, beyond just summarizing the original article.

In this case, I’ve come up with my own way forward. There are actually concrete skills I’d like to teach. They’re skills that link up with what the textbook is teaching, skills grounded in the concepts it’s trying to convey, and that makes me think I can convey them. It will give some structure to the lesson, a focus on not merely what I’d like the students to think but what I’d like them to do.

I won’t go into too much detail: I suspect some of the students may be reading this, and I don’t want to spoil the surprise! But I’m looking forward to class, and to getting to try another pedagogical experiment.

Jumpstarting Elliptic Bootstrapping

Leave a reply

I was at a mini-conference this week, called Jumpstarting Elliptic Bootstrap Methods for Scattering Amplitudes.

I’ve done a lot of work with what we like to call “bootstrap” methods. Instead of doing a particle physics calculation in all its gory detail, we start with a plausible guess and impose requirements based on what we know. Eventually, we have the right answer pulled up “by its own bootstraps”: the only answer the calculation could have, without actually doing the calculation.

This method works very well, but so far it’s only been applied to certain kinds of calculations, involving mathematical functions called polylogarithms. More complicated calculations involve a mathematical object called an elliptic curve, and until very recently it wasn’t clear how to bootstrap them. To get people thinking about it, my colleagues Hjalte Frellesvig and Andrew McLeod asked the Carlsberg Foundation (yes, that Carlsberg) to fund a mini-conference. The idea was to get elliptic people and bootstrap people together (along with Hjalte’s tribe, intersection theory people) to hash things out. “Jumpstart people” are not a thing in physics, so despite the title they were not invited.

Anyone remember these games? Did you know that they still exist, have an educational MMO, and bought neopets?

Having the conference so soon after the yearly Elliptics meeting had some strange consequences. There was only one actual duplicate talk, but the first day of talks all felt like they would have been welcome additions to the earlier conference. Some might be functioning as “overflow”: Elliptics this year focused on discussion and so didn’t have many slots for talks, while this conference despite its discussion-focused goal had a more packed schedule. In other cases, people might have been persuaded by the more relaxed atmosphere and lack of recording or posted slides to give more speculative talks. Oliver Schlotterer’s talk was likely in this category, a discussion of the genus-two functions one step beyond elliptics that I think people at the previous conference would have found very exciting, but which involved work in progress that I could understand him being cautious about presenting.

The other days focused more on the bootstrap side, with progress on some surprising but not-quite-yet elliptic avenues. It was great to hear that Mark Spradlin is making new progress on his Ziggurat story, to hear James Drummond suggest a picture for cluster algebras that could generalize to other theories, and to get some idea of the mysterious ongoing story that animates my colleague Cristian Vergu.

There was one thing the organizers couldn’t have anticipated that ended up throwing the conference into a new light. The goal of the conference was to get people started bootstrapping elliptic functions, but in the meantime people have gotten started on their own. Roger Morales Espasa presented his work on this with several of my other colleagues. They can already reproduce a known result, the ten-particle elliptic double-box, and are well on-track to deriving something genuinely new, the twelve-particle version. It’s exciting, but it definitely makes the rest of us look around and take stock. Hopefully for the better!

Cabinet of Curiosities: The Nested Toy

Leave a reply

I had a paper two weeks ago with a Master’s student, Alex Chaparro Pozo. I haven’t gotten a chance to talk about it yet, so I thought I should say a few words this week. It’s another entry in what I’ve been calling my cabinet of curiosities, interesting mathematical “objects” I’m sharing with the world.

I calculate scattering amplitudes, formulas that give the probability that particles scatter off each other in particular ways. While in principle I could do this with any particle physics theory, I have a favorite: a “toy model” called N=4 super Yang-Mills. N=4 super Yang-Mills doesn’t describe reality, but it lets us figure out cool new calculation tricks, and these often end up useful in reality as well.

Many scattering amplitudes in N=4 super Yang-Mills involve a type of mathematical functions called polylogarithms. These functions are especially easy to work with, but they aren’t the whole story. One we start considering more complicated situations (what if two particles collide, and eight particles come out?) we need more complicated functions, called elliptic polylogarithms.

A few years ago, some collaborators and I figured out how to calculate one of these elliptic scattering amplitudes. We didn’t do it as well as we’d like, though: the calculation was “half-done” in a sense. To do the other half, we needed new mathematical tools, tools that came out soon after. Once those tools were out, we started learning how to apply them, trying to “finish” the calculation we started.

The original calculation was pretty complicated. Two particles colliding, eight particles coming out, meant that in total we had to keep track of ten different particles. That gets messy fast. I’m pretty good at dealing with six particles, not ten. Luckily, it turned out there was a way to pretend there were six particles only: by “twisting” up the calculation, we found a toy model within the toy model: a six-particle version of the calculation. Much like the original was in a theory that doesn’t describe the real world, these six particles don’t describe six particles in that theory: they’re a kind of toy calculation within the toy model, doubly un-real.

Not quintuply-unreal though

With this nested toy model, I was confident we could do the calculation. I wasn’t confident I’d have time for it, though. This ended up making it perfect for a Master’s thesis, which is how Alex got into the game.

Alex worked his way through the calculation, programming and transforming, going from one type of mathematical functions to another (at least once because I’d forgotten to tell him the right functions to use, oops!) There were more details and subtleties than expected, but in the end everything worked out.

Then, we were scooped.

Another group figured out how to do the full, ten-particle problem, not just the toy model. That group was just “down the hall”…or would have been “down the hall” if we had been going to the office (this was 2021, after all). I didn’t hear about what they were working on until it was too late to change plans.

Alex left the field (not, as far as I know, because of this). And for a while, because of that especially thorough scooping, I didn’t publish.

What changed my mind, in part, was seeing the field develop in the meantime. It turns out toy models, and even nested toy models, are quite useful. We still have a lot of uncertainty about what to do, how to use the new calculation methods and what they imply. And usually, the best way to get through that kind of uncertainty is with simple, well-behaved toy models.

So I thought, in the end, that this might be useful. Even if it’s a toy version of something that already exists, I expect it to be an educational toy, one we can learn a lot from. So I’ve put it out into the world, as part of this year’s cabinet of curiosities.