Monthly Archives: August 2015

Romeo and Juliet, through a Wormhole

2 Replies

Perimeter is hosting this year’s Mathematica Summer School on Theoretical Physics. The school is a mix of lectures on a topic in physics (this year, the phenomenon of quantum entanglement) and tips and tricks for using the symbolic calculation program Mathematica.

Juan Maldacena is one of the lecturers, which gave me a chance to hear his Romeo and Juliet-based explanation of the properties of wormholes. While I’ve criticized some of Maldacena’s science popularization work in the past, this one is pretty solid, so I thought I’d share it with you guys.

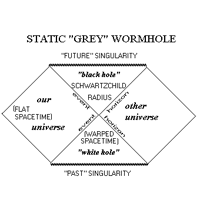
You probably think of wormholes as “shortcuts” to travel between two widely separated places. As it turns out, this isn’t really accurate: while “normal” wormholes do connect distant locations, they don’t do it in a way that allows astronauts to travel between them, Interstellar-style. This can be illustrated with something called a Penrose diagram:

Static

Static “Greyish Black” Diagram

In the traditional Penrose diagram, time goes upward, while space goes from side to side. In order to measure both in the same units, we use the speed of light, so one year on the time axis corresponds to one light-year on the space axis. This means that if you’re traveling at a 45 degree line on the diagram, you’re going at the speed of light. Any lower angle is impossible, while any higher angle means you’re going slower.

If we start in “our universe” in the diagram, can we get to the “other universe”?

Pretty clearly, the answer is no. As long as we go slower than the speed of light, when we pass the event horizon of the wormhole we will end up, not in the “other universe”, but at the part of the diagram labeled Future Singularity, the singularity at the center of the black hole. Even going at the speed of light only keeps us orbiting the event horizon for all eternity, at best.

What use could such a wormhole be? Well, imagine you’re Romeo or Juliet.

Romeo has been banished from Verona, but he took one end of a wormhole with him, while the other end was left with Juliet. He can’t go through and visit her, she can’t go through and visit him. But if they’re already considering taking poison, there’s an easier way. If they both jump in to the wormhole, they’ll fall in to the singularity. Crucially, though, it’s the same singularity, so once they’re past the event horizon they can meet inside the black hole, spending some time together before the end.

Depicted here for more typical quantum protagonists, Alice and Bob.

This explains what wormholes really are: two black holes that share a center.

Why was Maldacena talking about this at a school on entanglement? Maldacena has recently conjectured that quantum entanglement and wormholes are two sides of the same phenomenon, that pairs of entangled particles are actually connected by wormholes. Crucially, these wormholes need to have the properties described above: you can’t use a pair of entangled particles to communicate information faster than light, and you can’t use a wormhole to travel faster than light. However, it is the “shared” singularity that ends up particularly useful, as it suggests a solution to the problem of black hole firewalls.

Firewalls were originally proposed as a way of getting around a particular paradox relating three states connected by quantum entanglement: a particle inside a black hole, radiation just outside the black hole, and radiation far away from the black hole. The way the paradox is set up, it appears that these three states must all be connected. As it turns out, though, this is prohibited by quantum mechanics, which only allows two states to be entangled at a time. The original solution proposed for this was a “firewall”, a situation in which anyone trying to observe all three states would “burn up” when crossing the event horizon, thus avoiding any observed contradiction. Maldacena’s conjecture suggests another way: if someone interacts with the far-away radiation, they have an effect on the black hole’s interior, because the two are connected by a wormhole! This ends up getting rid of the contradiction, allowing the observer to view the black hole and distant radiation as two different descriptions of the same state, and it depends crucially on the fact that a wormhole involves a shared singularity.

There’s still a lot of detail to be worked out, part of the reason why Maldacena presented this research here was to inspire more investigation from students. But it does seem encouraging that Romeo and Juliet might not have to face a wall of fire before being reunited.

The Theorist Exclusion Principle

6 Replies

There are a lot of people who think theoretical physics has gone off-track, though very few of them agree on exactly how. Some think that string theory as a whole is a waste of time, others that the field just needs to pay more attention to their preferred idea. Some think we aren’t paying enough attention to the big questions, or that we’re too focused on “safe” ideas like supersymmetry, even when they aren’t working out. Some think the field needs less focus on mathematics, while others think it needs even more.

Usually, people act on these opinions by writing strongly worded articles and blog posts. Sometimes, they have more power, and act with money, creating grants and prizes that only go to their preferred areas of research.

Let’s put the question of whether the field actually needs to change aside for the moment. Even if it does, I’m skeptical that this sort of thing will have any real effect. While grants and blogs may be very good at swaying experimentalists, theorists are likely to be harder to shift, due to what I’m going to call the Theorist Exclusion Principle.

The Pauli Exclusion Principle is a rule from quantum mechanics that states that two fermions (particles with half-integer spin) can’t occupy the same state. Fermions include electrons, quarks, protons…essentially, all the particles that make up matter. Many people learn about the Pauli Exclusion Principle first in a chemistry class, where it explains why electrons fall into different energy levels in atoms: once one energy level “fills up”, no more electrons can occupy the same state, and any additional electrons are “excluded” and must occupy a different energy level.

Those 1s electrons are such a clique!

In contrast, bosons (like photons, or the Higgs) can all occupy the same state. It’s what allows for things like lasers, and it’s why all the matter we’re used to is made out of fermions: because fermions can’t occupy the same state as each other, as you add more fermions the structures they form have to become more and more complicated.

Experimentalists are a little like bosons. While you can’t stuff two experimentalists into the same quantum state, you can get them working on very similar projects. They can form large collaborations, with each additional researcher making the experiment that much easier. They can replicate eachother’s work, making sure it was accurate. They can take some physical phenomenon and subject it to a battery of tests, so that someone is bound to learn something.

Theorists, on the other hand, are much more like fermions. In theory, there’s very little reason to work on something that someone else is already doing. Replication doesn’t mean very much: the purest theory involves mathematical proofs, where replication is essentially pointless. Theorists do form collaborations, but they don’t have the same need for armies of technicians and grad students that experimentalists do. With no physical objects to work on, there’s a limit to how much can be done pursuing one particular problem, and if there really are a lot of options they can be pursued by one person with a cluster.

Like fermions, then, theorists expand to fill the projects available. If an idea is viable, someone will probably work on it, and once they do, there isn’t much reason for someone else to do the same thing.

This makes theory a lot harder to influence than experiment. You can write the most beautiful thinkpiece possible to persuade theorists to study the deep questions of the universe, but if there aren’t any real calculations available nothing will change. Contrary to public perception, theoretical physicists aren’t paid to just sit around thinking all day: we calculate, compute, and publish, and if a topic doesn’t lend itself to that then we won’t get much mileage out of it. And no matter what you try to preferentially fund with grants, mostly you’ll just get people re-branding what they’re already doing, shifting a few superficial details to qualify.

Theorists won’t occupy the same states, so if you want to influence theorists you need to make sure there are open states where you’re trying to get them to go. Historically, theorists have shifted when new states have opened up: new data from experiment that needed a novel explanation, new mathematical concepts that opened up new types of calculations. You want there to be fewer string theorists, or more focus on the deep questions? Give us something concrete to do, and I guarantee you’ll get theorists flooding in.

Want to Open up Your Work? Try a Data Mine!

Leave a reply

Have you heard of the Open Science movement?

The general idea is to make scientists’ work openly accessible, both to the general public and to other scientists. This doesn’t just include published results, but the raw data as well. The goal is to make it possible for anyone, in principle, to check the validity of important results.

I’m of the opinion that this sort of thing isn’t always feasible, but when it is it’s usually a great thing to do. And in my field, the best way to do this sort of thing is to build a data mine.

I’m thinking in particular of Blümlein, Broadhurst, and Vermaseren’s Multiple Zeta Value Data Mine. Multiple zeta values are the result of generalizing the Riemann Zeta Function, and evaluating it at one. They’re transcendental numbers, and there are complicated relations between them. Finding all those relations, even for a restricted subset of them, can be a significant task. Usually, there aren’t published programs for this sort of thing, like most things in physics we have to jury-rig up our own code. What makes the folks behind the multiple zeta value data mine unique is that when they had to do this, they didn’t just keep the code to themselves. Instead, they polished it up and put it online.

That’s the general principle behind building a data mine. By putting your tools online, you make them available to others, so other researchers can use them as a jumping-off point for their own work. This can speed up the field, bringing everyone up to the same starting point, and has the side benefit of gathering heaps of citations from people who use your tools.

My collaborators already have a site with some of the data from our research into hexagon functions. Originally, it was just a place to house extra-large files that couldn’t be included with the original paper. For our next paper, we’re planning on expanding it into a true data mine, and including enough technology for someone else to build off of our results.

Historic Montreal

1 Reply

I’m at a conference in Montreal this week, so it’s going to be a short post. The University of Montreal’s Centre de Recherches Mathématiques has been holding a program on the various hidden symmetries of N=4 super Yang-Mills since the beginning of the summer. This week is the amplitudes-focused part of the program, so they’ve brought in a bunch of amplitudes-folks from around the world, myself included.

It’s been great hanging out with fellow members of my sub-field, as always, both at the conference and at dinner afterwards. Over possibly too much wine I heard stories of the heady days of 2007, when James Drummond and Johannes Henn first discovered one of the most powerful symmetries of N=4 super Yang-Mills (a duality called dual conformal invariance) and Andrew Hodges showed off the power of a set of funky variables called twistors. It’s amazing to me how fast the field moves, sometimes: by the time I started doing amplitudes work in 2011 these ideas were the bedrock of the field. History operates on different scales, and in amplitudes a few decades have played host to an enormous amount of progress.

History in the real world can move surprisingly fast too. After seeing cathedrals in Zurich that date back to the medieval era, I was surprised when the majestic basilica overlooking Montreal turned out to be less than a century old.

In retrospect the light-up cross should have made it obvious.

In retrospect the light-up cross should have made it obvious.