Category Archives: Gravity

Post on the Weak Gravity Conjecture for FirstPrinciples.org

I have another piece this week on the FirstPrinciples.org Hub. If you’d like to know who they are, I say a bit about my impressions of them in my post on the last piece I had there. They’re still finding their niche, so there may be shifts in the kind of content they cover over time, but for now they’ve given me an opportunity to cover a few topics that are off the beaten path.

This time, the piece is what we in the journalism biz call an “explainer”. Instead of interviewing people about cutting-edge science, I wrote a piece to explain an older idea. It’s an idea that’s pretty cool, in a way I think a lot of people can actually understand: a black hole puzzle that might explain why gravity is the weakest force. It’s an idea that’s had an enormous influence, both in the string theory world where it originated and on people speculating more broadly about the rules of quantum gravity. If you want to learn more, read the piece!

Since I didn’t interview anyone for this piece, I don’t have the same sort of “bonus content” I sometimes give. Instead of interviewing, I brushed up on the topic, and the best resource I found was this review article written by Dan Harlow, Ben Heidenreich, Matthew Reece, and Tom Rudelius. It gave me a much better idea of the subtleties: how many different ways there are to interpret the original conjecture, and how different attempts to build on it reflect on different facets and highlight different implications. If you are a physicist curious what the whole thing is about, I recommend reading that review: while I try to give a flavor of some of the subtleties, a piece for a broad audience can only do so much.

Why Quantum Gravity Is Controversial

27 Replies

Merging quantum mechanics and gravity is a famously hard physics problem. Explaining why merging quantum mechanics and gravity is hard is, in turn, a very hard science communication problem. The more popular descriptions tend to lead to misunderstandings, and I’ve posted many times over the years to chip away at those misunderstandings.

Merging quantum mechanics and gravity is hard…but despite that, there are proposed solutions. String Theory is supposed to be a theory of quantum gravity. Loop Quantum Gravity is supposed to be a theory of quantum gravity. Asymptotic Safety is supposed to be a theory of quantum gravity.

One of the great virtues of science and math is that we are, eventually, supposed to agree. Philosophers and theologians might argue to the end of time, but in math we can write down a proof, and in science we can do an experiment. If we don’t yet have the proof or the experiment, then we should reserve judgement. Either way, there’s no reason to get into an unproductive argument.

Despite that, string theorists and loop quantum gravity theorists and asymptotic safety theorists, famously, like to argue! There have been bitter, vicious, public arguments about the merits of these different theories, and decades of research doesn’t seem to have resolved them. To an outside observer, this makes quantum gravity seem much more like philosophy or theology than like science or math.

Why is there still controversy in quantum gravity? We can’t do quantum gravity experiments, sure, but if that were the problem physicists could just write down the possibilities and leave it at that. Why argue?

Some of the arguments are for silly aesthetic reasons, or motivated by academic politics. Some are arguments about which approaches are likely to succeed in future, which as always is something we can’t actually reliably judge. But the more justified arguments, the strongest and most durable ones, are about a technical challenge. They’re about something called non-perturbative physics.

Most of the time, when physicists use a theory, they’re working with an approximation. Instead of the full theory, they’re making an assumption that makes the theory easier to use. For example, if you assume that the velocity of an object is small, you can use Newtonian physics instead of special relativity. Often, physicists can systematically relax these assumptions, including more and more of the behavior of the full theory and getting a better and better approximation to the truth. This process is called perturbation theory.

Other times, this doesn’t work well. The full theory has some trait that isn’t captured by the approximations, something that hides away from these systematic tools. The theory has some important aspect that is non-perturbative.

Every proposed quantum gravity theory uses approximations like this. The theory’s proponents try to avoid these approximations when they can, but often they have to approximate and hope they don’t miss too much. The opponents, in turn, argue that the theory’s proponents are missing something important, some non-perturbative fact that would doom the theory altogether.

Asymptotic Safety is built on top of an approximation, one different from what other quantum gravity theorists typically use. To its proponents, work using their approximation suggests that gravity works without any special modifications, that the theory of quantum gravity is easier to find than it seems. Its opponents aren’t convinced, and think that the approximation is missing something important which shows that gravity needs to be modified.

In Loop Quantum Gravity, the critics think their approximation misses space-time itself. Proponents of Loop Quantum Gravity have been unable to prove that their theory, if you take all the non-perturbative corrections into account, doesn’t just roll up all of space and time into a tiny spiky ball. They expect that their theory should allow for a smooth space-time like we experience, but the critics aren’t convinced, and without being able to calculate the non-perturbative physics neither side can convince the other.

String Theory was founded and originally motivated by perturbative approximations. Later, String Theorists figured out how to calculate some things non-perturbatively, often using other simplifications like supersymmetry. But core questions, like whether or not the theory allows a positive cosmological constant, seem to depend on non-perturbative calculations that the theory gives no instructions for how to do. Some critics don’t think there is a consistent non-perturbative theory at all, that the approximations String Theorists use don’t actually approximate to anything. Even within String Theory, there are worries that the theory might try to resist approximation in odd ways, becoming more complicated whenever a parameter is small enough that you could use it to approximate something.

All of this would be less of a problem with real-world evidence. Many fields of science are happy to use approximations that aren’t completely rigorous, as long as those approximations have a good track record in the real world. In general though, we don’t expect evidence relevant to quantum gravity any time soon. Maybe we’ll get lucky, and studies of cosmology will reveal something, or an experiment on Earth will have a particularly strange result. But nature has no obligation to help us out.

Without evidence, though, we can still make mathematical progress. You could imagine someone proving that the various perturbative approaches to String Theory become inconsistent when stitched together into a full non-perturbative theory. Alternatively, you could imagine someone proving that a theory like String Theory is unique, that no other theory can do some key thing that it does. Either of these seems unlikely to come any time soon, and most researchers in these fields aren’t pursuing questions like that. But the fact the debate could be resolved means that it isn’t just about philosophy or theology. There’s a real scientific, mathematical controversy, one rooted in our inability to understand these theories beyond the perturbative methods their proponents use. And while I don’t expect it to be resolved any time soon, one can always hold out hope for a surprise.

Gravity-Defying Theories

5 Replies

Universal gravitation was arguably Newton’s greatest discovery. Newton realized that the same laws could describe the orbits of the planets and the fall of objects on Earth, that bodies like the Moon can be fully understood only if you take into account both the Earth and the Sun’s gravity. In a Newtonian world, every mass attracts every other mass in a tiny, but detectable way.

Einstein, in turn, explained why. In Einstein’s general theory of relativity, gravity comes from the shape of space and time. Mass attracts mass, but energy affects gravity as well. Anything that can be measured has a gravitational effect, because the shape of space and time is nothing more than the rules by which we measure distances and times. So gravitation really is universal, and has to be universal.

…except when it isn’t.

It turns out, physicists can write down theories with some odd properties. Including theories where things are, in a certain sense, immune to gravity.

The story started with two mathematicians, Shiing-Shen Chern and Jim Simons. Chern and Simons weren’t trying to say anything in particular about physics. Instead, they cared about classifying different types of mathematical space. They found a formula that, when added up over one of these spaces, counted some interesting properties of that space. A bit more specifically, it told them about the space’s topology: rough details, like the number of holes in a donut, that stay the same even if the space is stretched or compressed. Their formula was called the Chern-Simons Form.

The physicist Albert Schwarz saw this Chern-Simons Form, and realized it could be interpreted another way. He looked at it as a formula describing a quantum field, like the electromagnetic field, describing how the field’s energy varied across space and time. He called the theory describing the field Chern-Simons Theory, and it was one of the first examples of what would come to be known as topological quantum field theories.

In a topological field theory, every question you might want to ask can be answered in a topological way. Write down the chance you observe the fields at particular strengths in particular places, and you’ll find that the answer you get only depends on the topology of the space the fields occupy. The answers are the same if the space is stretched or squished together. That means that nothing you ask depends on the details of how you measure things, that nothing depends on the detailed shape of space and time. Your theory is, in a certain sense, independent of gravity.

Others discovered more theories of this kind. Edward Witten found theories that at first looked like they depend on gravity, but where the gravity secretly “cancels out”, making the theory topological again. It turned out that there were many ways to “twist” string theory to get theories of this kind.

Our world is for the most part not described by a topological theory, gravity matters! (Though it can be a good approximation for describing certain materials.) These theories are most useful, though, in how they allow physicists and mathematicians to work together. Physicists don’t have a fully mathematically rigorous way of defining most of their theories, just a series of approximations and an overall picture that’s supposed to tie them together. For a topological theory, though, that overall picture has a rigorous mathematical meaning: it counts topological properties! As such, topological theories allow mathematicians to prove rigorous results about physical theories. It means they can take a theory of quantum fields or strings that has a particular property that physicists are curious about, and find a version of that property that they can study in fully mathematical rigorous detail. It’s been a boon both to mathematicians interested in topology, and to physicists who want to know more about their theories.

So while you won’t have antigravity boots any time soon, theories that defy gravity are still useful!

Cause and Effect and Stories

Solutions and Solutions

3 Replies

The best misunderstandings are detective stories. You can notice when someone is confused, but digging up why can take some work. If you manage, though, you learn much more than just how to correct the misunderstanding. You learn something about the words you use, and the assumptions you make when using them.

Recently, someone was telling me about a book they’d read on Karl Schwarzschild. Schwarzschild is famous for discovering the equations that describe black holes, based on Einstein’s theory of gravitation. To make the story more dramatic, he did so only shortly before dying from a disease he caught fighting in the first World War. But this person had the impression that Schwarzschild had done even more. According to this person, the book said that Schwarzschild had done something to prove Einstein’s theory, or to complete it.

Another Schwarzschild accomplishment: that mustache

At first, I thought the book this person had read was wrong. But after some investigation, I figured out what happened.

The book said that Schwarzschild had found the first exact solution to Einstein’s equations. That’s true, and as a physicist I know precisely what it means. But I now realize that the average person does not.

In school, the first equations you solve are algebraic, x+y=z. Some equations, like x^2=4, have solutions. Others, like x^2=-4, seem not to, until you learn about new types of numbers that solve them. Either way, you get used to equations being like a kind of puzzle, a question for which you need to find an answer.

If you’re thinking of equations like that, then it probably sounds like Schwarzschild “solved the puzzle”. If Schwarzschild found the first solution to Einstein’s equation, that means that Einstein did not. That makes it sound like Einstein’s work was incomplete, that he had asked the right question but didn’t yet know the right answer.

Einstein’s equations aren’t algebraic equations, though. They’re differential equations. Instead of equations for a variable, they’re equations for a mathematical function, a formula that, in this case, describes the curvature of space and time.

Scientists in many fields use differential equations, but they use them in different ways. If you’re a chemist or a biologist, it might be that you’re most used to differential equations with simple solutions, like sines, cosines, or exponentials. You learn how to solve these equations, and they feel a bit like the algebraic ones: you have a puzzle, and then you solve the puzzle.

Other fields, though, have tougher differential equations. If you’re a physicist or an engineer, you’ve likely met differential equations that you can’t treat in this way. If you’re dealing with fluid mechanics, or general relativity, or even just Newtonian gravity in an odd situation, you can’t usually solve the problem by writing down known functions like sines and cosines.

That doesn’t mean you can’t solve the problem at all, though!

Even if you can’t write down a solution to a differential equation with sines and cosines, a solution can still exist. (In some cases, we can even prove a solution exists!) It just won’t be written in terms of sines and cosines, or other functions you’ve learned in school. Instead, the solution will involve some strange functions, functions no-one has heard of before.

If you want, you can make up names for those functions. But unless you’re going to classify them in a useful way, there’s not much point. Instead, you work with these functions by approximation. You calculate them in a way that doesn’t give you the full answer, but that does let you estimate how close you are. That’s good enough to give you numbers, which in turn is good enough to compare to experiments. With just an approximate solution, like this, Einstein could check if his equations described the orbit of Mercury.

Once you know you can find these approximate solutions, you have a different perspective on equations. An equation isn’t just a mysterious puzzle. If you can approximate the solution, then you already know how to solve that puzzle. So we wouldn’t think of Einstein’s theory as incomplete because he was only able to find approximate solutions: for a theory as complicated as Einstein’s, that’s perfectly normal. Most of the time, that’s all we need.

But it’s still pretty cool when you don’t have to do this. Sometimes, we can not just approximate, but actually “write down” the solution, either using known functions or well-classified new ones. We call a solution like that an analytic solution, or an exact solution.

That’s what Schwarzschild managed. These kinds of exact solutions often only work in special situations, and Schwarzschild’s is no exception. His Schwarzschild solution works for matter in a special situation, arranged in a perfect sphere. If matter happened to be arranged in that way, then the shape of space and time would be exactly as Schwarzschild described it.

That’s actually pretty cool! Einstein’s equations are complicated enough that no-one was sure that there were any solutions like that, even in very special situations. Einstein expected it would be a long time until they could do anything except approximate solutions.

(If Schwarzschild’s solution only describes matter arranged in a perfect sphere, why do we think it describes real black holes? This took later work, by people like Roger Penrose, who figured out that matter compressed far enough will always find a solution like Schwarzschild’s.)

Schwarzschild intended to describe stars with his solution, or at least a kind of imaginary perfect star. What he found was indeed a good approximation to real stars, but also the possibility that a star shoved into a sufficiently small space would become something weird and new, something we would come to describe as a black hole. That’s a pretty impressive accomplishment, especially for someone on the front lines of World War One. And if you know the difference between an exact solution and an approximate one, you have some idea of what kind of accomplishment that is.

LHC Black Holes for the Terminally Un-Reassured

12 Replies

Could the LHC have killed us all?

No, no it could not.

But…

I’ve had this conversation a few times over the years. Usually, the people I’m talking to are worried about black holes. They’ve heard that the Large Hadron Collider speeds up particles to amazingly high energies before colliding them together. They worry that these colliding particles could form a black hole, which would fall into the center of the Earth and busily gobble up the whole planet.

This pretty clearly hasn’t happened. But also, physicists were pretty confident that it couldn’t happen. That isn’t to say they thought it was impossible to make a black hole with the LHC. Some physicists actually hoped to make a black hole: it would have been evidence for extra dimensions, curled-up dimensions much larger than the tiny ones required by string theory. They figured out the kind of evidence they’d see if the LHC did indeed create a black hole, and we haven’t seen that evidence. But even before running the machine, they were confident that such a black hole wouldn’t gobble up the planet. Why?

The best argument is also the most unsatisfying. The LHC speeds up particles to high energies, but not unprecedentedly high energies. High-energy particles called cosmic rays enter the atmosphere every day, some of which are at energies comparable to the LHC. The LHC just puts the high-energy particles in front of a bunch of sophisticated equipment so we can measure everything about them. If the LHC could destroy the world, cosmic rays would have already done so.

That’s a very solid argument, but it doesn’t really explain why. Also, it may not be true for future colliders: we could build a collider with enough energy that cosmic rays don’t commonly meet it. So I should give another argument.

The next argument is Hawking radiation. In Stephen Hawking’s most famous accomplishment, he argued that because of quantum mechanics black holes are not truly black. Instead, they give off a constant radiation of every type of particle mixed together, shrinking as it does so. The radiation is faintest for large black holes, but gets more and more intense the smaller the black hole is, until the smallest black holes explode into a shower of particles and disappear. This argument means that a black hole small enough that the LHC could produce it would radiate away to nothing in almost an instant: not long enough to leave the machine, let alone fall to the center of the Earth.

This is a good argument, but maybe you aren’t as sure as I am about Hawking radiation. As it turns out, we’ve never measured Hawking radiation, it’s just a theoretical expectation. Remember that the radiation gets fainter the larger the black hole is: for a black hole in space with the mass of a star, the radiation is so tiny it would be almost impossible to detect even right next to the black hole. From here, in our telescopes, we have no chance of seeing it.

So suppose tiny black holes didn’t radiate, and suppose the LHC could indeed produce them. Wouldn’t that have been dangerous?

Here, we can do a calculation. I want you to appreciate how tiny these black holes would be.

From science fiction and cartoons, you might think of a black hole as a kind of vacuum cleaner, sucking up everything nearby. That’s not how black holes work, though. The “sucking” black holes do is due to gravity, no stronger than the gravity of any other object with the same mass at the same distance. The only difference comes when you get close to the event horizon, an invisible sphere close-in around the black hole. Pass that line, and the gravity is strong enough that you will never escape.

We know how to calculate the position of the event horizon of a black hole. It’s the Schwarzchild radius, and we can write it in terms of Newton’s constant G, the mass of the black hole M, and the speed of light c, as follows:

$\frac{2GM}{c^2}$

The Large Hadron Collider’s two beams each have an energy around seven tera-electron-volts, or TeV, so there are 14 TeV of energy in total in each collision. Imagine all of that energy being converted into mass, and that mass forming a black hole. That isn’t how it would actually happen: some of the energy would create other particles, and some would give the black hole a “kick”, some momentum in one direction or another. But we’re going to imagine a “worst-case” scenario, so let’s assume all the energy goes to form the black hole. Electron-volts are a weird physicist unit, but if we divide them by the speed of light squared (as we should if we’re using 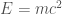$E=mc^2$ to create a mass), then Wikipedia tells us that each electron-volt will give us $1.78\times 10^{-36}$ kilograms. “Tera” is the SI prefix for $10^{12}$ . 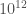Thus our tiny black hole starts with a mass of

$14\times 10^{12}\times 1.78\times 10^{-36} = 2.49\times 10^{-23} \textrm{kg}$

Plugging in Newton’s constant (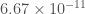 $6.67\times 10^{-11}$ meters cubed per kilogram per second squared), and the speed of light ( 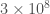$3\times 10^8$ meters per second), and we get a radius of,

$\frac{2\times 6.67\times 10^{-11}\times 14\times 10^{12}\times 1.78\times 10^{-36}}{\left(3\times 10^8\right)^2} = 3.7\times 10^{-50} \textrm{m}$

That, by the way, is amazingly tiny. The size of an atom is about $10^{-10}$ meters. If every atom was a tiny person, and each of that person’s atoms was itself a person, and so on for five levels down, then the atoms of the smallest person would be the same size as this event horizon.

Now, we let this little tiny black hole fall. Let’s imagine it falls directly towards the center of the Earth. The only force affecting it would be gravity (if it had an electrical charge, it would quickly attract a few electrons and become neutral). That means you can think of it as if it were falling through a tiny hole, with no friction, gobbling up anything unfortunate enough to fall within its event horizon.

For our first estimate, we’ll treat the black hole as if it stays the same size through its journey. Imagine the black hole travels through the entire earth, absorbing a cylinder of matter. Using the Earth’s average density of 5515 kilograms per cubic meter, and the Earth’s maximum radius of 6378 kilometers, our cylinder adds a mass of,

$\pi \times \left(3.7\times 10^{-50}\right)^2 \times 2 \times 6378\times 10^3\times 5515 = 3\times 10^{-88} \textrm{kg}$

That’s absurdly tiny. That’s much, much, much tinier than the mass we started out with. Absorbing an entire cylinder through the Earth makes barely any difference.

You might object, though, that the black hole is gaining mass as it goes. So really we ought to use a differential equation. If the black hole travels a distance r, absorbing mass as it goes at average Earth density 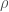$\rho$ , then we find,

$\frac{dM}{dr}=\pi\rho\left(\frac{2GM(r)}{c^2}\right)^2$

Solving this, we get

$M(r)=\frac{M_0}{1- M_0 \pi\rho\left(\frac{2G}{c^2}\right)^2 r }$

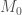Where $M_0$ is the mass we start out with.

Plug in the distance through the Earth for r, and we find…still about 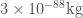$3\times 10^{-88} \textrm{kg}$ ! It didn’t change very much, which makes sense, it’s a very very small difference!

But you might still object. A black hole falling through the Earth wouldn’t just go straight through. It would pass through, then fall back in. In fact, it would oscillate, from one side to the other, like a pendulum. This is actually a common problem to give physics students: drop an object through a hole in the Earth, neglect air resistance, and what does it do? It turns out that the time the object takes to travel through the Earth is independent of its mass, and equal to roughly 84.5 minutes.

So let’s ask a question: how long would it take for a black hole, oscillating like this, to double its mass?

We want to solve,

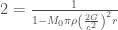
$2=\frac{1}{1- M_0 \pi\rho\left(\frac{2G}{c^2}\right)^2 r }$

so we need the black hole to travel a total distance of

$r=\frac{1}{2M_0 \pi\rho\left(\frac{2G}{c^2}\right)^2} = 5.3\times 10^{71} \textrm{m}$

That’s a huge distance! The Earth’s radius, remember, is 6378 kilometers. So traveling that far would take

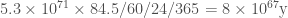
$5.3\times 10^{71} \times 84.5/60/24/365 = 8\times 10^{67} \textrm{y}$

Ten to the sixty-seven years. Our universe is only about ten to the ten years old. In another five times ten to the nine years, the Sun will enter its red giant phase, and swallow the Earth. There simply isn’t enough time for this tiny tiny black hole to gobble up the world, before everything is already gobbled up by something else. Even in the most pessimistic way to walk through the calculation, it’s just not dangerous.

I hope that, if you were worried about black holes at the LHC, you’re not worried any more. But more than that, I hope you’ve learned three lessons. First, that even the highest-energy particle physics involves tiny energies compared to day-to-day experience. Second, that gravitational effects are tiny in the context of particle physics. And third, that with Wikipedia access, you too can answer questions like this. If you’re worried, you can make an estimate, and check!

The Problem of Quantum Gravity Is the Problem of High-Energy (Density) Quantum Gravity

21 Replies

I’ve said something like this before, but here’s another way to say it.

The problem of quantum gravity is one of the most famous problems in physics. You’ve probably heard someone say that quantum mechanics and general relativity are fundamentally incompatible. Most likely, this was narrated over pictures of a foaming, fluctuating grid of space-time. Based on that, you might think that all we have to do to solve this problem is to measure some quantum property of gravity. Maybe we could make a superposition of two different gravitational fields, see what happens, and solve the problem that way.

I mean, we could do that, some people are trying to. But it won’t solve the problem. That’s because the problem of quantum gravity isn’t just the problem of quantum gravity. It’s the problem of high-energy quantum gravity.

Merging quantum mechanics and general relativity is actually pretty easy. General relativity is a big conceptual leap, certainly, a theory in which gravity is really just the shape of space-time. At the same time, though, it’s also a field theory, the same general type of theory as electromagnetism. It’s a weirder field theory than electromagnetism, to be sure, one with deeper implications. But if we want to describe low energies, and weak gravitational fields, then we can treat it just like any other field theory. We know how to write down some pretty reasonable-looking equations, we know how to do some basic calculations with them. This part is just not that scary.

The scary part happens later. The theory we get from these reasonable-looking equations continues to look reasonable for a while. It gives formulas for the probability of things happening: things like gravitational waves bouncing off each other, as they travel through space. The problem comes when those waves have very high energy, and the nice reasonable probability formula now says that the probability is greater than one.

For those of you who haven’t taken a math class in a while, probabilities greater than one don’t make sense. A probability of one is a certainty, something guaranteed to happen. A probability greater than one isn’t more certain than certain, it’s just nonsense.

So we know something needs to change, we know we need a new theory. But we only know we need that theory when the energy is very high: when it’s the Planck energy. Before then, we might still have a different theory, but we might not: it’s not a “problem” yet.

Now, a few of you understand this part, but still have a misunderstanding. The Planck energy seems high for particle physics, but it isn’t high in an absolute sense: it’s about the energy in a tank of gasoline. Does that mean that all we have to do to measure quantum gravity is to make a quantum state out of your car?

Again, no. That’s because the problem of quantum gravity isn’t just the problem of high-energy quantum gravity either.

Energy seems objective, but it’s not. It’s subjective, or more specifically, relative. Due to special relativity, observers moving at different speeds observe different energies. Because of that, high energy alone can’t be the requirement: it isn’t something either general relativity or quantum field theory can “care about” by itself.

Instead, the real thing that matters is something that’s invariant under special relativity. This is hard to define in general terms, but it’s best to think of it as a requirement for not energy, but energy density.

(For the experts: I’m justifying this phrasing in part because of how you can interpret the quantity appearing in energy conditions as the energy density measured by an observer. This still isn’t the correct way to put it, but I can’t think of a better way that would be understandable to a non-technical reader. If you have one, let me know!)

Why do we need quantum gravity to fully understand black holes? Not just because they have a lot of mass, but because they have a lot of mass concentrated in a small area, a high energy density. Ditto for the Big Bang, when the whole universe had a very large energy density. Particle colliders are useful not just because they give particles high energy, but because they give particles high energy and put them close together, creating a situation with very high energy density.

Once you understand this, you can use it to think about whether some experiment or observation will help with the problem of quantum gravity. Does the experiment involve very high energy density, much higher than anything we can do in a particle collider right now? Is that telescope looking at something created in conditions of very high energy density, or just something nearby?

It’s not impossible for an experiment that doesn’t meet these conditions to find something. Whatever the correct quantum gravity theory is, it might be different from our current theories in a more dramatic way, one that’s easier to measure. But the only guarantee, the only situation where we know we need a new theory, is for very high energy density.

Simulated Wormhole Analogies

3 Replies

Last week, I talked about how Google’s recent quantum simulation of a toy model wormhole was covered in the press. What I didn’t say much about, was my own opinion of the result. Was the experiment important? Was it worth doing? Did it deserve the hype?

Here on this blog, I don’t like to get into those kinds of arguments. When I talk about public understanding of science, I share the same concerns as the journalists: we all want to prevent misunderstandings, and to spread a clearer picture. I can argue that some choices hurt the public understanding and some help it, and be reasonably confident that I’m saying something meaningful, something that would resonate with their stated values.

For the bigger questions, what goals science should have and what we should praise, I have much less of a foundation. We don’t all have a clear shared standard for which science is most important. There isn’t some premise I can posit, a fundamental principle I can use to ground a logical argument.

That doesn’t mean I don’t have an opinion, though. It doesn’t even mean I can’t persuade others of it. But it means the persuasion has to be a bit more loose. For example, I can use analogies.

So let’s say I’m looking at a result like this simulated wormhole. Researchers took advanced technology (Google’s quantum computer), and used it to model a simple system. They didn’t learn anything especially new about that system (since in this case, a normal computer can simulate it better). I get the impression they didn’t learn all that much about the advanced technology: the methods used, at this point, are pretty well-known, at least to Google. I also get the impression that it wasn’t absurdly expensive: I’ve seen other people do things of a similar scale with Google’s machine, and didn’t get the impression they had to pay through the nose for the privilege. Finally, the simple system simulated happens to be “cool”: it’s a toy model studied by quantum gravity researchers, a simple version of that sci-fi standard, the traversible wormhole.

What results are like that?

Occasionally, scientists build tiny things. If the tiny things are cute enough, or cool enough, they tend to get media attention. The most recent example I can remember was a tiny snowman, three microns tall. These tiny things tend to use very advanced technology, and it’s hard to imagine the scientists learn much from making them, but it’s also hard to imagine they cost all that much to make. They’re amusing, and they absolutely get press coverage, spreading wildly over the web. I don’t think they tend to get published in Nature unless they are a bit more advanced, but I wouldn’t be too surprised if I heard of a case that did, scientific journals can be suckers for cute stories too. They don’t tend to get discussed in glowing terms linking them to historical breakthroughs.

That seems like a pretty close analogy. Taken seriously, it would suggest the wormhole simulation was probably worth doing, probably worth a press release and some media coverage, likely not worth publication in Nature, and definitely not worth being heralded as a major breakthrough.

Ok, but proponents of the experiment might argue I’m leaving something out here. This experiment isn’t just a cute simulation. It’s supposed to be a proof of principle, an early version of an experiment that will be an actually useful simulation.

As an analogy for that…did you know LIGO started taking data in 2002?

Most people first heard of the Laser Interferometer Gravitational-Wave Observatory in 2016, when they reported their first detection of gravitational waves. But that was actually “advanced LIGO”. The original LIGO ran from 2002 to 2010, and didn’t detect anything. It just wasn’t sensitive enough. Instead, it was a prototype, an early version designed to test the basic concept.

Similarly, while this wormhole situation didn’t teach anything new, future ones might. If the quantum simulation was made larger, it might be possible to simulate more complicated toy models, ones that are too complicated to simulate on a normal computer. These aren’t feasible now, but may be feasible with somewhat bigger quantum computers: still much smaller than the computers that would be needed to break encryption, or even to do simulations that are useful for chemists and materials scientists. Proponents argue that some of these quantum toy models might teach them something interesting about the mathematics of quantum gravity.

Here, though, a number of things weaken the analogy.

LIGO’s first run taught them important things about the noise they would have to deal with, things that they used to build the advanced version. The wormhole simulation didn’t show anything novel about how to use a quantum computer: the type of thing they were doing was well-understood, even if it hadn’t been used to do that yet.

Detecting gravitational waves opened up a new type of astronomy, letting us observe things we could never have observed before. For these toy models, it isn’t obvious to me that the benefit is so unique. Future versions may be difficult to classically simulate, but it wouldn’t surprise me if theorists figured out how to understand them in other ways, or gained the same insight from other toy models and moved on to new questions. They’ll have a while to figure it out, because quantum computers aren’t getting bigger all that fast. I’m very much not an expert in this type of research, so maybe I’m wrong about this…but just comparing to similar research programs, I would be surprised if the quantum simulations end up crucial here.

Finally, even if the analogy held, I don’t think it proves very much. In particular, as far as I can tell, the original LIGO didn’t get much press. At the time, I remember meeting some members of the collaboration, and they clearly didn’t have the fame the project has now. Looking through google news and the archives of the New York times, I can’t find all that much about the experiment: a few articles discussing its progress and prospects, but no grand unveiling, no big press releases.

So ultimately, I think viewing the simulation as a proof of principle makes it, if anything, less worth the hype. A prototype like that is only really valuable when it’s testing new methods, and only in so far as the thing it’s a prototype for will be revolutionary. Recently, a prototype fusion device got a lot of press for getting more energy out of a plasma than they put into it (though still much less than it takes to run the machine). People already complained about that being overhyped, and the simulated wormhole is nowhere near that level of importance.

If anything, I think the wormhole-simulators would be on a firmer footing if they thought of their work like the tiny snowmen. It’s cute, a fun side benefit of advanced technology, and as such something worth chatting about and celebrating a bit. But it’s not the start of a new era.

The Undefinable

11 Replies

If I can teach one lesson to all of you, it’s this: be precise. In physics, we try to state what we mean as precisely as we can. If we can’t state something precisely, that’s a clue: maybe what we’re trying to state doesn’t actually make sense.

Someone recently reached out to me with a question about black holes. He was confused about how they were described, about what would happen when you fall in to one versus what we could see from outside. Part of his confusion boiled down to a question: “is the center really an infinitely small point?”

I remembered a commenter a while back who had something interesting to say about this. Trying to remind myself of the details, I dug up this question on Physics Stack Exchange. user4552 has a detailed, well-referenced answer, with subtleties of General Relativity that go significantly beyond what I learned in grad school.

According to user4552, the reason this question is confusing is that the usual setup of general relativity cannot answer it. In general relativity, singularities like the singularity in the middle of a black hole aren’t treated as points, or collections of points: they’re not part of space-time at all. So you can’t count their dimensions, you can’t see whether they’re “really” infinitely small points, or surfaces, or lines…

This might surprise people (like me) who have experience with simpler equations for these things, like the Schwarzchild metric. The Schwarzchild metric describes space-time around a black hole, and in the usual coordinates it sure looks like the singularity is at a single point where r=0, just like the point where r=0 is a single point in polar coordinates in flat space. The thing is, though, that’s just one sort of coordinates. You can re-write a metric in many different sorts of coordinates, and the singularity in the center of a black hole might look very different in those coordinates. In general relativity, you need to stick to things you can say independent of coordinates.

Ok, you might say, so the usual mathematics can’t answer the question. Can we use more unusual mathematics? If our definition of dimensions doesn’t tell us whether the singularity is a point, maybe we just need a new definition!

According to user4552, people have tried this…and it only sort of works. There are several different ways you could define the dimension of a singularity. They all seem reasonable in one way or another. But they give different answers! Some say they’re points, some say they’re three-dimensional. And crucially, there’s no obvious reason why one definition is “right”. The question we started with, “is the center really an infinitely small point?”, looked like a perfectly reasonable question, but it actually wasn’t: the question wasn’t precise enough.

This is the real problem. The problem isn’t that our question was undefined, after all, we can always add new definitions. The problem was that our question didn’t specify well enough the definitions we needed. That is why the question doesn’t have an answer.

Once you understand the difference, you see these kinds of questions everywhere. If you’re baffled by how mass could have come out of the Big Bang, or how black holes could radiate particles in Hawking radiation, maybe you’ve heard a physicist say that energy isn’t always conserved. Energy conservation is a consequence of symmetry, specifically, symmetry in time. If your space-time itself isn’t symmetric (the expanding universe making the past different from the future, a collapsing star making a black hole), then you shouldn’t expect energy to be conserved.

I sometimes hear people object to this. They ask, is it really true that energy isn’t conserved when space-time isn’t symmetric? Shouldn’t we just say that space-time itself contains energy?

And well yes, you can say that, if you want. It isn’t part of the usual definition, but you can make a new definition, one that gives energy to space-time. In fact, you can make more than one new definition…and like the situation with the singularity, these definitions don’t always agree! Once again, you asked a question you thought was sensible, but it wasn’t precise enough to have a definite answer.

Keep your eye out for these kinds of questions. If scientists seem to avoid answering the question you want, and keep answering a different question instead…it might be their question is the only one with a precise answer. You can define a method to answer your question, sure…but it won’t be the only way. You need to ask precise enough questions to get good answers.

Duality and Emergence: When Is Spacetime Not Spacetime?

21 Replies

Spacetime is doomed! At least, so say some physicists. They don’t mean this as a warning, like some comic-book universe-destroying disaster, but rather as a research plan. These physicists believe that what we think of as space and time aren’t the full story, but that they emerge from something more fundamental, so that an ultimate theory of nature might not use space or time at all. Other, grumpier physicists are skeptical. Joined by a few philosophers, they think the “spacetime is doomed” crowd are over-excited and exaggerating the implications of their discoveries. At the heart of the argument is the distinction between two related concepts: duality and emergence.

In physics, sometimes we find that two theories are actually dual: despite seeming different, the patterns of observations they predict are the same. Some of the more popular examples are what we call holographic theories. In these situations, a theory of quantum gravity in some space-time is dual to a theory without gravity describing the edges of that space-time, sort of like how a hologram is a 2D image that looks 3D when you move it. For any question you can ask about the gravitational “bulk” space, there is a matching question on the “boundary”. No matter what you observe, neither description will fail.

If theories with gravity can be described by theories without gravity, does that mean gravity doesn’t really exist? If you’re asking that question, you’re asking whether gravity is emergent. An emergent theory is one that isn’t really fundamental, but instead a result of the interaction of more fundamental parts. For example, hydrodynamics, the theory of fluids like water, emerges from more fundamental theories that describe the motion of atoms and molecules.

(For the experts: I, like most physicists, am talking about “weak emergence” here, not “strong emergence”.)

The “spacetime is doomed” crowd think that not just gravity, but space-time itself is emergent. They expect that distances and times aren’t really fundamental, but a result of relationships that will turn out to be more fundamental, like entanglement between different parts of quantum fields. As evidence, they like to bring up dualities where the dual theories have different concepts of gravity, number of dimensions, or space-time. Using those theories, they argue that space and time might “break down”, and not be really fundamental.

(I’ve made arguments like that in the past too.)

The skeptics, though, bring up an important point. If two theories are really dual, then no observation can distinguish them: they make exactly the same predictions. In that case, say the skeptics, what right do you have to call one theory more fundamental than the other? You can say that gravity emerges from a boundary theory without gravity, but you could just as easily say that the boundary theory emerges from the gravity theory. The whole point of duality is that no theory is “more true” than the other: one might be more or less convenient, but both describe the same world. If you want to really argue for emergence, then your “more fundamental” theory needs to do something extra: to predict something that your emergent theory doesn’t predict.

Sometimes this is a fair objection. There are members of the “spacetime is doomed” crowd who are genuinely reckless about this, who’ll tell a journalist about emergence when they really mean duality. But many of these people are more careful, and have thought more deeply about the question. They tend to have some mix of these two perspectives:

First, if two descriptions give the same results, then do the descriptions matter? As physicists, we have a history of treating theories as the same if they make the same predictions. Space-time itself is a result of this policy: in the theory of relativity, two people might disagree on which one of two events happened first or second, but they will agree on the overall distance in space-time between the two. From this perspective, a duality between a bulk theory and a boundary theory isn’t evidence that the bulk theory emerges from the boundary, but it is evidence that both the bulk and boundary theories should be replaced by an “overall theory”, one that treats bulk and boundary as irrelevant descriptions of the same physical reality. This perspective is similar to an old philosophical theory called positivism: that statements are meaningless if they cannot be derived from something measurable. That theory wasn’t very useful for philosophers, which is probably part of why some philosophers are skeptics of “space-time is doomed”. The perspective has been quite useful to physicists, though, so we’re likely to stick with it.

Second, some will say that it’s true that a dual theory is not an emergent theory…but it can be the first step to discover one. In this perspective, dualities are suggestive evidence that a deeper theory is waiting in the wings. The idea would be that one would first discover a duality, then discover situations that break that duality: examples on one side that don’t correspond to anything sensible on the other. Maybe some patterns of quantum entanglement are dual to a picture of space-time, but some are not. (Closer to my sub-field, maybe there’s an object like the amplituhedron that doesn’t respect locality or unitarity.) If you’re lucky, maybe there are situations, or even experiments, that go from one to the other: where the space-time description works until a certain point, then stops working, and only the dual description survives. Some of the models of emergent space-time people study are genuinely of this type, where a dimension emerges in a theory that previously didn’t have one. (For those of you having a hard time imagining this, read my old post about “bubbles of nothing”, then think of one happening in reverse.)

It’s premature to say space-time is doomed, at least as a definite statement. But it is looking like, one way or another, space-time won’t be the right picture for fundamental physics. Maybe that’s because it’s equivalent to another description, redundant embellishment on an essential theoretical core. Maybe instead it breaks down, and a more fundamental theory could describe more situations. We don’t know yet. But physicists are trying to figure it out.

4 gravitons

Stories about physics from someone who's been there