Last week I talked about the history of neutrinos. Neutrinos come in three types, or “flavors”. Electron neutrinos are the easiest: they’re produced alongside electrons and positrons in the different types of beta decay. Electrons have more massive cousins, called muon and tau particles. As it turns out, each of these cousins has a corresponding flavor of neutrino: muon neutrinos, and tau neutrinos.
For quite some time, physicists thought that all of these neutrinos had zero mass.
(If the idea of a particle with zero mass confuses you, think about photons. A particle with zero mass travels, like a photon, at the speed of light. This doesn’t make them immune to gravity: just as no light can escape a black hole, neither can any other massless particle. It turns out that once you take into account Einstein’s general theory of relativity, gravity cares about energy, not just mass.)
Eventually, physicists started to realize they were wrong, and neutrinos had a small non-zero mass after all. Their reason why might seem a bit strange, though. Physicists didn’t weigh the neutrinos, or measure their speed. Instead, they observed that different flavors of neutrinos transform into each other. We say that they oscillate: electron neutrinos oscillate into muon or tau neutrinos, which oscillate into the other flavors, and so on. Over time, a beam of electron neutrinos will become a beam of mostly tau and muon neutrinos, before becoming a beam of electron neutrinos again.
That might not sound like it has much to do with mass. To understand why it does, you’ll need to learn this post’s lesson:
Lesson 2: Mass is just How Particles Move
Oscillating particles seem like a weird sort of evidence for mass. What would be a more normal kind of evidence?
Those of you who’ve taken physics classes might remember the equation . Apply a known force to something, see how much it accelerates, and you can calculate its mass. If you’ve had a bit more physics, you’ll know that this isn’t quite the right equation to use for particles close to the speed of light, but that there are other equations we can use in a similar way. In particular, using relativity, we have
. (At rest,
, and we have the famous
). This lets us do the same kind of thing: give something a kick and see how it moves.
So let’s say we do that: we give a particle a kick, and measure it later. I’ll visualize this with a tool physicists use called a Feynman diagram. The line represents a particle traveling from one side to the other, from “kick” to “measurement”:
Because we only measure the particle at the end, we might miss if something happens in between. For example, it might interact with another particle or field, like this:
If we don’t know about this other field, then when we try to measure the particle’s mass we will include interactions like this. As it turns out, this is how the Higgs boson works: the Higgs field interacts with particles like electrons and quarks, changing how they move, so that they appear to have mass.
Quantum particles can do other things too. You might have heard people talk about one particle turning into a pair of temporary “virtual particles”. When people say that, they usually have a diagram in mind like this:
In particle physics, we need to take into account every diagram of this kind, every possible thing that could happen in between “kick” and measurement. The final result isn’t one path or another, but a sum of all the different things that could have happened in between. So when we measure the mass of a particle, we’re including every diagram that’s allowed: everything that starts with our “kick” and ends with our measurement.
Now what if our particle can transform, from one flavor to another?
Now we have a new type of thing that can happen in between “kick” and measurement. And if it can happen once, it can happen more than once:
Remember that, when we measure mass, we’re measuring a sum of all the things that can happen in between. That means our particle could oscillate back and forth between different flavors many many times, and we need to take every possibility into account. Because of that, it doesn’t actually make sense to ask what the mass is for one flavor, for just electron neutrinos or just muon neutrinos. Instead, mass is for the thing that actually moves: an average (actually, a quantum superposition) over all the different flavors, oscillating back and forth any number of times.
When a process like beta decay produces an electron neutrino, the thing that actually moves is a mix (again, a superposition) of particles with these different masses. Because each of these masses respond to their initial “kick” in different ways, you see different proportions of them over time. Try to measure different flavors at the end, and you’ll find different ones depending on when and where you measure. That’s the oscillation effect, and that’s why it means that neutrinos have mass.
It’s a bit more complicated to work out the math behind this, but not unreasonably so: it’s simpler than a lot of other physics calculations. Working through the math, we find that by measuring how long it takes neutrinos to oscillate we can calculate the differences between (squares of) neutrino masses. What we can’t calculate are the masses themselves. We know they’re small: neutrinos travel at almost the speed of light, and our cosmological models of the universe have surprisingly little room for massive neutrinos: too much mass, and our universe would look very different than it does today. But we don’t know much more than that. We don’t even know the order of the masses: you might assume electron neutrinos are on average lighter than muon neutrinos, which are lighter than tau neutrinos…but it could easily be the other way around! We also don’t know whether neutrinos get their mass from the Higgs like other particles do, or if they work in a completely different way.
Unlike other mysteries of physics, we’ll likely have the answer to some of these questions soon. People are already picking through the data from current experiments, seeing if they hint towards one order of masses or the other, or to one or the other way for neutrinos to get their mass. More experiments will start taking data this year, and others are expected to start later this decade. At some point, the textbooks may well have more “normal” mass numbers for each of the neutrinos. But until then, they serve as a nice illustration of what mass actually means in particle physics.






I loved this explanation-could you go into more discussion about what the equations themselves mean? Thank you for sharing!
LikeLike
There are two equations I used in this post,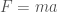 and
and  . The first one goes back to Newton (though he didn’t write it that way), and is how force relates to motion in Newton’s understanding of physics. You apply a force,
. The first one goes back to Newton (though he didn’t write it that way), and is how force relates to motion in Newton’s understanding of physics. You apply a force, 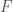 to a mass
to a mass 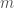 , and it accelerates (gets faster) with acceleration
, and it accelerates (gets faster) with acceleration  . The second equation is the relationship between energy, mass, and momentum in Einstein’s theory of relativity. It tells you that the energy of an object comes both from its movement (described by its momentum
. The second equation is the relationship between energy, mass, and momentum in Einstein’s theory of relativity. It tells you that the energy of an object comes both from its movement (described by its momentum  ) and by its mass
) and by its mass 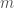 .
.
I don’t know if that’s the sort of explanation you were looking for (or if you meant to ask about the diagrams instead!) If you say a bit about your physics background I can see if I can give you a better explanation.
LikeLike
Love the way you used color in the diagrams! It’s simple, but not many people do it.
LikeLiked by 1 person
There is , also , the notion of proper time in Relativity for everything that has a rest mass , so , unlike photons , it can ” experience” some kind of change in its own reference frame.
Neutrinos are quantum entities of course , like every other particle , so these classical intuitions like proper time are not that ” proper” for them , but , anyway , QFTs already incorporate special relativity , so this analogy ( for the neutrino oscillations as a kind of change in proper time
) may not be that ” off”.
LikeLike
I can explain the topics in the post at a much deeper level of nature, if any are willing to listen. Here is a tidbit of what I have to offer. Nature has been very tricky to decipher and I know why physicists have been confused about the solution for 150 years. It comes down to point charges, maximum electromagnetic field strength, and the structures that emerge when these point charges are mixed over a vast range of different continuous electromagnetic and kinetic energies, the structures they form, and the emergent discretization of the quantum unit of energy. The emergent structures which implement Einstein’s spacetime and the standard model particles. Your article describes a set of the biggest clues in nature. The neutrino exhibits oscillation of energy and mass. Except physicists don’t yet understand the concept of apparent energy and they also don’t understand how mass emerges. I can explain this all in a way that I think will be obvious, if someone will just listen. p.s., I think you can also adapt string theory and then immediately be in the lead with a mathematical model. The loop quantum gravity folks will be close on your heels, as will the Bohmian mechanics folks. They can all be adapted to this new paradigm. One big excitement is looking forward to the new mathematics and simulation solutions that will emerge based on the point charge paradigm establishing new ‘fundamentals’. There may be more beyond these new fundamentals, questions we may not be able to answer even, yet now we have a pathway to distance order of magnitude 10^-35. Anyone want to listen?
LikeLike