When talking science, we need to be careful with our words. It’s easy for people to see a familiar word and assume something totally different from what we intend. And if we use the same word twice, for two different things…
I’ve noticed this problem with the word “integral”. When physicists talk about particle physics, there are two kinds of integrals we mention: path integrals, and loop integrals. I’ve seen plenty of people get confused, and assume that these two are the same thing. They’re not, and it’s worth spending some time explaining the difference.
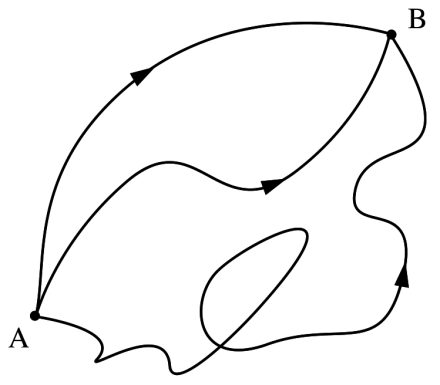
Let’s start with path integrals (also referred to as functional integrals, or Feynman integrals). Feynman promoted a picture of quantum mechanics in which a particle travels along many different paths, from point A to point B.
You’ve probably seen a picture like this. Classically, a particle would just take one path, the shortest path, from A to B. In quantum mechanics, you have to add up all possible paths. Most longer paths cancel, so on average the short, classical path is the most important one, but the others do contribute, and have observable, quantum effects. The sum over all paths is what we call a path integral.
It’s easy enough to draw this picture for a single particle. When we do particle physics, though, we aren’t usually interested in just one particle: we want to look at a bunch of different quantum fields, and figure out how they will interact.
We still use a path integral to do that, but it doesn’t look like a bunch of lines from point A to B, and there isn’t a convenient image I can steal from Wikipedia for it. The quantum field theory path integral adds up, not all the paths a particle can travel, but all the ways a set of quantum fields can interact.
How do we actually calculate that?
One way is with Feynman diagrams, and (often, but not always) loop integrals.
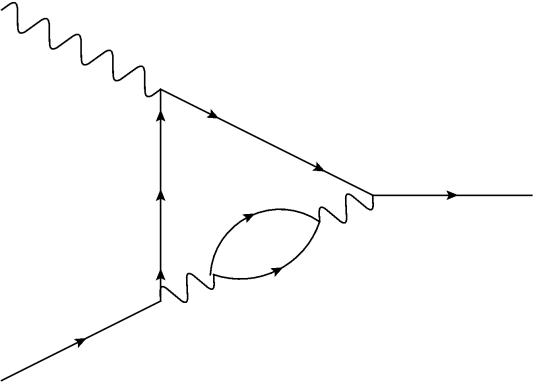
I’ve talked about Feynman diagrams before. Each one is a picture of one possible way that particles can travel, or that quantum fields can interact. In some (loose) sense, each one is a single path in the path integral.
Each diagram serves as instructions for a calculation. We take information about the particles, their momenta and energy, and end up with a number. To calculate a path integral exactly, we’d have to add up all the diagrams we could possibly draw, to get a sum over all possible paths.
(There are ways to avoid this in special cases, which I’m not going to go into here.)
Sometimes, getting a number out of a diagram is fairly simple. If the diagram has no closed loops in it (if it’s what we call a tree diagram) then knowing the properties of the in-coming and out-going particles is enough to know the rest. If there are loops, though, there’s uncertainty: you have to add up every possible momentum of the particles in the loops. You do that with a different integral, and that’s the one that we sometimes refer to as a loop integral. (Perhaps confusingly, these are also often called Feynman integrals: Feynman did a lot of stuff!)
Loop integrals can be pretty complicated, but at heart they’re the same sort of thing you might have seen in a calculus class. Mathematicians are pretty comfortable with them, and they give rise to numbers that mathematicians find very interesting.
Path integrals are very different. In some sense, they’re an “integral over integrals”, adding up every loop integral you could write down. Mathematicians can define path integrals in special cases, but it’s still not clear that the general case, the overall path integral picture we use, actually makes rigorous mathematical sense.
So if you see physicists talking about integrals, it’s worth taking a moment to figure out which one we mean. Path integrals and loop integrals are both important, but they’re very, very different things.
Sorry but in physics jargon, path integrals and Feynman integrals are exactly synonymous. Both phrases apply both to the integration over trajectories of one particle x(t); as well as integration over fields phi(x,y,z,t).
After all, the former is just the special 0+1-dimensional case of the latter. And the multi-particle extension of the former is equivalent to the latter – after all, both may be used as the starting point to derive Feynman diagrams.
Your claim that these are “totally different” concepts is just totally wrong and the reasons that lead you to create a whole blog post out of this misinformation seem baffling.
The only thing that could be “totally different” is the contour integration – that someone might sloppily call “path integral” as well. That’s of course a vastly simpler concept. But path integrals, Feynman integrals, and functional integrals are equally complex – and at the qualitative level, exactly synonymous.
LikeLiked by 1 person
I’m using “Feynman integral” here as shorthand for “Feynman parameter integral”, which is a fairly common shorthand in the amplitudes literature and in popular articles about amplitudes.
LikeLiked by 1 person
Yup, I understood that, perhaps after I posted my comment. But the Feynman integral is also a normal name for the path integral. For example, Wikipedia redirects “Feynman integral” to a path integral page, EncyclopediaOfMath dot org has a page “Feynman integral” that is also about path integrals, and mentions that it’s also a name for a finite-dimensional integral, and Scholarpedia says it may mean both.
Now I understand that your choice is dominant in the amplitude industry but you can’t extend it beyond that field. By the way, Feynman heard something about “Feynman integrals” at a 1979 conference. The speaker probably meant what you mean. Feynman asked: “What is a Feynman integral?” He was generally opposed to such jargon that requires one to be “very careful” of terminology.
This is a terminological debate so it’s a pure convention who is “right”. It depends on which authorities or vague arguments you place at the top. But the main problem I have with your view probably starts already in your sentence “one has to be careful with words”. I think that people should use the words in such a way that they don’t have to be careful with words unless there is some real subtlety that makes it unavoidable to be careful. When you use a confusing name “Feynman integral” for something, people must be careful about phrases even if it’s not necessary, and that’s a sign of a badly chosen terminology.
LikeLiked by 2 people
If someone else could chime in and say whether they were confused by this, that would be helpful. It’s easy enough for me to replace “Feynman integral” in this piece with, say, “loop integral” if this is a common point of confusion.
LikeLiked by 1 person
I wasn’t confused by it, but that might come from the fact that in all the discussions I’ve had about this we’ve always reserved the term “Feynman integral” for the general evaluation of a Feynman diagram and “path integral” or “functional integral” for the path integral itself. I can’t think of a time where I’ve seen Feynman integral refer to the path integral by itself, usually it’s been phrased as “Feynman’s path integral”.
LikeLiked by 2 people
I wasn’t confused. But, to use an educational cliche, it is useful to “teach the controversy.”
In my day job of law (which I also teach to lawyers and paralegals for continuing education credits), one of the constant frustrations I face is the mistaken belief that a word has one and only one meaning without regard to context, which is rarely the case, even with fairly commonly used ordinary words like “shall”, which sound precise (that controversy is for another day).
Both you and Lubos seems to be falling prey to that fallacy, even though both of you have stated in no uncertain terms that respectable native speakers of physics-ese use the term “Feynman integral” in an inconsistent manner, and even though each of you, who are each professionally trained physicists in sub-fields of physics that uses this term, can’t even agree on which of the two senses of the word is correct and which is not. When a situation like that arises, you are both wrong, at least from a descriptivist linguist’s perspective, because both of your are insisting that the word has only one sense, when, in fact, it has two.
A great many words have different meanings when used in different contexts. This holds true even in technical fields with words like a “Feynman integral”. It may have an original meaning, and when it is used differently from the original meaning, at first, that secondary sense of the phrase may be incorrect. But, once enough credible people have used it intentionally in each of two senses, both meanings become correct, and a reader has to be aware that the phrase has more than one meaning so that the reader can be alert to the possible meanings and can take care to grok which one is being used in which context (which is usually obvious, but not always, especially in short communications).
This isn’t limited to technical words only used in obscure ways either. For example, the American English meaning of the word “billion” is 1,000,000,000, but the British English meaning of the same word is 1,000,000,000,000. Unless you know which dialect of English your author uses and which audience your author has in mind, the word “billion” is frequently ambiguous, and that term is used in also sorts of disciplines by all sorts of people.
LikeLiked by 3 people
This is why cosmologists speak of “gigayears” rather than “billion years”
LikeLiked by 2 people
Thanks for the feedback. I’ve gone ahead and swapped the wording, as well as adding some parentheticals about other terms people use.
For the record, I have no particular attachment to “Feynman integral” as referring only to loop integrals, it’s the usage I’m familiar with, and I honestly forgot that people sometimes drop the “path” in “Feynman path integral”. It still seemed like the context made it reasonably clear which one I was talking about, so I wanted to get independent confirmation that the post was confusing because Lubos has a history of misreading my posts in…unique…ways.
LikeLiked by 2 people
If by a loop integral, you mean some integral over loop momenta or the equivalent in the position representation, I don’t agree that many people confuse this term with the path integral. Why should they? And who are they? Do you have some example of the people who confused them? People may confuse many things with each other but I don’t find it particularly helpful to invent confusions that actually don’t exist – the number of things that real people are actually confused about is high enough.
LikeLiked by 1 person