Monthly Archives: January 2013

So what do you actually do?

Leave a reply

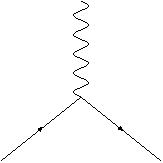
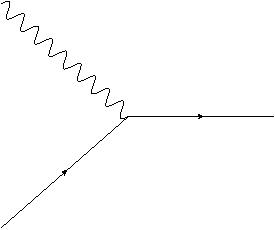
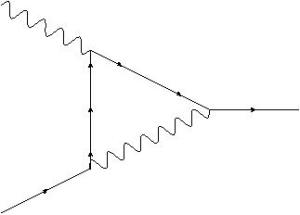
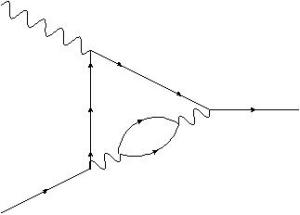
A few days ago, my sister asked me what I do at work. What do I actually do in order to do my job? What sort of tasks does it involve?

I answered by showing her this:

WhatIDo

Needless to say, that wasn’t very helpful, so I thought a bit and now I have a better answer.

Doing theoretical physics is basically like doing homework. In particular, it’s like doing difficult, interesting homework.

Think of the toughest homework assignment you’ve ever had to do. A homework assignment so tough, you and all your friends in the class worked together to finish it, and none of you were sure you were going to get it right.

Chances are, you handled the situation in one of two ways, depending on whether this was a group project, or an individual one.

Group Project:

This is what you do when you’re supposed to be in a group. Maybe you’re putting together a presentation, or building a rocket. Whatever you’re doing, you’ve got a lot of little tasks that need to get done in order to achieve your goals, so you parcel them out: each group member is assigned a specific task, and at the end everyone meets and puts it all together.

This sort of situation is common in theoretical physics as well, and it happens when different people have different skills to contribute. If one theorist is good at programming, while another understands a particular esoteric type of mathematics, then the math person will do the calculations and then give the results to the programming person, who makes a program to implement it.

Individual Project:

On the other hand, if everyone needs to submit their own work, you can’t very well just do part of it (not without cheating, anyway). Still, it’s not as if you’re doing this on your own. You do your own work to solve the problem, but you keep in contact with your classmates, and when you get stuck, you ask one of them for help.

This sort of situation happens in theoretical physics when everyone is relatively on the same page. Everyone works through the problem individually, doing the calculation and making their own programs, and whenever someone gets stuck, they talk to the others. Everyone periodically compares their results, which serves as a cross-check to make sure nobody made a mistake. The only difference from doing homework is that you and your collaborators write your own problems…which means, none of you know if there is a solution!

In both cases (group and individual), theoretical physics is a matter of doing calculations, writing programs, and thinking through thought experiments. Sometimes that means specific tasks as part of one huge project; sometimes it means working side by side on the same calculation. Either way, it all boils down to one thing: I’m someone who does homework for a living.

Some thoughts about the current Flame Challenge

Leave a reply

Ever tried to explain something to an eleven year old?

It’s not the same as talking to a six year old. There’s no need to talk down, or to oversimplify: eleven is smart enough to understand most of what you have to say. On the other hand, most eleven year olds haven’t had chemistry or physics, or algebra. They’re about as intelligent as they’re going to get, but with almost no knowledge base, which makes them a uniquely relevant challenge for communicating science.

That’s the concept behind Alan Alda’s Flame Challenge: eleven year olds around the country pick a question and scientists (via video, images, or text) attempt to answer it. Last year, the challenge question was “What is a flame?” a question from Alan Alda’s own youth. This year, the eleven year olds had their first opportunity to choose, and they chose a doozy: “What is time?”

This is…well, a difficult question. Not just hard to explain, it’s a question that could mean one of several different things. Alan Alda has embraced the ambiguity and assures contestants that they can pursue whichever interpretation they think best, but in the end the judges are eleven year olds around the country, and it will be their call whether an answer is sufficient.

(As an aside, I think this sort of ambiguous question isn’t a fluke: barring a new vetting procedure, we’re going to keep getting questions like this. If an eleven year old wants to understand something with a definite answer, he or she will just Google it. It’s only the ambiguous, tricky, arguably poorly-formed questions that can’t be answered by a quick search.)

I’ve been brainstorming a bit, and I’ve come up with a few meanings for the question “What is time?”

  • How should time travel work? In my own limited experience with kids asking about time, this is usually what they’re going for. Screw the big philosophical questions: can I go kill a dinosaur, and if I do, should I be worried that everyone will be speaking Chinese when I get back? In some ways this is the easiest question to answer because, barring Everett-style interpretations of quantum mechanics, there really is only one way for time travel to work consistent with current science, and that’s through wormholes. Wormholes aren’t an especially difficult concept: all they really require is some understanding of the idea that space can be curved. Flatland in particular proves ideal for teaching students to think of space as more than just three static directions, which is why I’m considering the (potentially wildly overambitious) idea of submitting an animated Flatland story dealing with wormholes and time travel for the Flame Challenge. By the way, any budding scientist-animators who are interested in collaborating on such a project are more than welcome! I’m not sure I can do this without help. By the way, one downside of this approach is that it is very well covered by movies and other media, so it is entirely possible that most eleven year olds know this already.
  • What makes time different from other dimensions? There is a flippant physicist answer to this question, and that is that time has a different sign in the Minkowski metric. What that means, in very vague terms, is that while rotations in space will always come back to where they started, if you rotate something in both space and time (it turns out all this means is gaining speed) you can keep going indefinitely, getting closer and closer to the speed of light without ever getting back to your previous speed. If you want to know why time is special like that, that’s harder to say, but occasionally papers bubble up on arXiv claiming that they understand why this should be the case. I’d love it if an author of one of those papers made a submission to the Flame Challenge.
  • Why does time have an arrow? Why does it only go forwards? This is not the same question as the previous one! This is much harder, and depending on who you talk to it relates somehow to entropy and thermodynamics or to quantum mechanics, or even to biology and psychology. It’s tricky to explain, but there have been many attempts, and I don’t doubt that a substantial number of the submissions will be in this vein.
  • How does Special Relativity (or General Relativity) work? How can time go faster or slower? This is a more specialized version of the question about why time is unique, and one that Alan Alda has made mention of in his interviews. Teaching Special Relativity or General Relativity to eleven year olds is a challenge, which is not to say it is impossible but rather the reverse: unlike the other questions, this is unambiguous enough that with enough work someone could do it, and possibly advance the field of science communication in doing so.
  • Is time real? Could time be an illusion? There are a number of variations of this, ranging from purely philosophical to directly scientific. Is it better to think of everything as happening at once, and our minds simply organizing it? Is time merely change, or could time exist in a changeless universe? There is a lot of ambiguity in answering this form of the question, and while we’ll see a few people trying to go in this vein I doubt there’s an answer that will satisfy the world’s eleven year olds.
  • Side topics. Someone could, of course, go on a completely different route. They could explain clocks, and timekeeping throughout the ages. They could talk about the definition of a second. They could talk about the beginning of time, and what that means, or discuss whether or not time had a beginning at all. They could talk about the relationship between energy and time, how one, via Noether’s Theorem, implies the other. There are many choices here, and the trick is to avoid straying too far from the main point. Eleven year olds are not forgiving folks, after all.

I am very much looking forward to seeing what people submit, and if all goes extraordinarily well, I may even have a submission too. It’s a very difficult topic this year, but we’re scientists! If anyone can do it, we can.

What’s so hard about Quantum Field Theory anyway?

5 Replies

As I have mentioned before a theory in theoretical physics can be described as a list of quantum fields and the ways in which they interact. It turns out this is all you need to start drawing Feynman Diagrams.

Feynman Diagrams are tools physicists use to calculate the probability of things happening: radioactive particles decaying, protons colliding, electrons changing course in a magnetic field…basically anything small enough that quantum mechanics is important. Each Feynman Diagram depicts the paths that a group of particles take over time, interacting as they go. It’s important to remember, however, that Feynman Diagrams are not literally what’s going on: rather, they are tools for calculation.

To start making a Feynman Diagram, think about what you need present in order to start whatever process you’re investigating. For the examples given above, this means a radioactive particle, two protons, and an electron and a magnetic field, respectively. For each particle or field that you start out with, draw a line on the left of the diagram.

4gravincoming

If you’re making a Feynman Diagram you’re looking for a probability of some particular outcome. Draw lines corresponding to the particles and fields in that outcome on the left of the diagram. For example, if you were looking at a radioactive decay, you’d want the new particles the original particle decayed into. For an electron moving in a magnetic field, you want the electron’s new path.

4gravoutgoing

Now come the interactions. Each way that the particles and fields can interact is a potential way that lines can come together. For example, electrons are affected by the photons that make up electric and magnetic fields. Specifically, an electron can absorb a photon, changing its path. This gives us an interaction: an electron and a photon go in, and an electron comes out.

4gravinteraction

You’ve got the basic building blocks: particles as lines, and interactions where the lines come together. Now, just link them all up! Something like this:

4gravclassical

Then again, you could also do it like this:

4gravanom

Or this:

4grav2loop

Or this:

4gravcomplicated

You get the idea. To use these diagrams, a physicist assigns a number to each line and each interaction, depending on various traits of the particles involved including their energy and angles of travel. For each diagram, all these numbers are multiplied together. Then, because in quantum mechanics every possible event has to be included, you add up all the numbers from all of the diagrams. Every single one.

Not just the simple diagram on the top, but also the more complicated one below it, and the one below that, and every way you could possibly link up all of the particles going in and coming out, each more and more complicated. An infinite list of diagrams. Only by adding all of those diagrams together can a physicist find the true, complete probability of a quantum event.

Adding an infinite set of increasingly complicated diagrams is tricky. By tricky, I mean nearly absolutely impossible and so insane in principle that mathematicians aren’t even sure that it has any real meaning.

Because of this, everything that physicists calculate is an approximation. This approximation is possible because each interaction multiplies the total for a diagram by a “small” number, which gets smaller the weaker the force involved, from around 1/2 for the strong nuclear force to about 1/12 for electricity and magnetism. If you limit the number of points of interaction, you limit the number of possible diagrams. For our example, limiting things to one point of interaction gives only the first diagram. If you allow up to three points, you get the second diagram, and so on. Each time you add two more interactions, your diagram gets another loop, and the contribution to the total is smaller, so that even just four loops with a force as weak as electricity and magnetism gets you all but a billionth of the total, which is about as accurate as the experiments are anyway.

What this means, though, is that we’re only at the very edge of a vast ocean of knowledge. We know the rules, the laws of physics if you will, but we can only tiptoe loop by loop towards the full formulas, sitting infinitely far away.

That, in essence, is what I work on. I look for patterns in the numbers, tricks in the calculation, ways to yank ourselves up by our bootstraps to higher and higher loops, and maybe, just maybe, for a shortcut up to infinity.

Because just because we know the rules, doesn’t mean we know how the game is played.

That’s Quantum Field Theory.

A Note on Blogging Style

Leave a reply

So I’ve come to realize that my blog posts have a somewhat odd format for a science blog, in that I tend to use paragraphs of only one or two sentences, with important points in bold.

While I somehow had the impression that this was a common style in science blogging, I haven’t seen it elsewhere, and a few weeks ago I figured out where it comes from: it’s the same style I use when writing D&D optimization handbooks.

In that field (if I may call it a field), it’s a fairly common writing style. It works well for its target audience, with short paragraphs to appeal to short attention spans and bolding to isolate the elementary concepts behind rules and advice. Liberal application of links and references then allows the reader to check up on the topic, each time increasing their knowledge of the subject’s wider context.

All of these seem like perfectly good things to cultivate in a science blog too!

My style may evolve over time, but I definitely think this is a good place to start. If you don’t like it, though, feel free to comment! If I’m not communicating with my readers, I’m not accomplishing very much, now am I?